Hoy, 15 de julio de 2017, ha muerto a la edad de 40 años Maryam Mirzakhani, matemática iraní ganadora de la Medalla Fields en 2014, el premio más importante otorgado en la disciplina. Pionera en muchísimos sentidos, fue la primera mujer en obtener dicho galardón (que se entrega desde 1936) y además la primera iraní. Sus investigaciones se centraban en la teoría de las superficies de Riemann y tienen profundas consecuencias en diversas áreas de las matemáticas, como los sistemas dinámicos, la geometría en todos sus sentidos y el análisis complejo. En Etilmercurio hemos decidido recordarla dando una breve revisión a su historia y a su trabajo.
Su vida
Mirzakhani nació en Teherán en 1977. Durante toda su juventud vivió bajo el inestable clima de la guerra entre Irán e Irak, pero a pesar de ello, pudo desarrollar sus estudios y ambiciones intelectuales gracias al apoyo de su familia. Su mayor interés durante su infancia, era la lectura y escritura, y no pensó en dedicarse seriamente a las matemáticas hasta el último año de su enseñanza media.
Durante su estadía en el colegio, conoció a múltiples personas que moldearon su interés por las matemáticas, entre los que destaca a su amiga Roya Beheshti, con la que iban a un mercado que quedaba cerca de su colegio, donde solo vendían libros. No les era permitido hojear los libros, así que simplemente aprovechaban los precios baratos y compraban libros al azar para leerlos.
A pesar de su curiosidad, Mirzakhani no destacó en matemáticas durante esos años de estudio y durante un par de ellos tuvo notas particularmente malas. Esto terminó con la llegada de una nueva profesora, quien la motivó e interesó en el estudio de matemáticas. Junto con su amiga Beheshti estudiaron para ser las seleccionadas de su colegio para participar en la IOI (International Olympiad in Informatics, Olimpiada Internacional de Informática), una competencia anual a nivel escolar sobre resolución de problemas informáticos.
Mirzakhani destaca a la directora de su colegio como una de las personas que más apoyó su dedicación a las matemáticas durante esta época. Ella era «una persona de carácter fuerte que estaba dispuesta a hacer lo que fuera necesario para darnos las mismas oportunidades que las que tienen el colegio de niños»; en un país donde no hay colegios mixtos en los años superiores de escolaridad [3]. Gracias a ella, Mirzakhani y Beheshti pudieron prepararse para nuevas competencias de matemáticas a nivel escolar y fueron las primeras mujeres partícipes del equipo iraní en las Olimpiadas Internacionales de Matemáticas. El esfuerzo rindió frutos: en 1994 y 1995 Mirzakhani se convirtió en la primera iraní en ganar dos medallas de oro y alcanzar puntaje perfecto en dichas olimpiadas. Este fue el empujón definitivo para decidir dedicarle su carrera a las matemáticas.
Luego de eso obtuvo su licenciatura en la Universidad de Tecnología de Sharif (Irán) en 1999, y en 2004 obtuvo su PhD en la Universidad de Harvard (Estados Unidos) bajo la tutela de Curtis McMullen, medallista Fields. Su tesis doctoral ya incluye uno de sus más grandes logros científicos al encontrar una fórmula asintótica para el número de geodésicas simples en superficies de Riemann; encontrando de paso una demostración alternativa a una importante conjetura de Witten. Luego trabajó en el Instituto Clay de Matemáticas y en la Universidad de Princeton antes de radicarse en la Universidad de Stanford en 2008 [1].
Su obra
Como se mencionó anteriormente, su trabajo se centraba en la teoría de las superficies de Riemann. Exponer de manera detallada su obra se escapa inmensamente del alcance de este artículo, por lo que expondremos de forma sucinta sólo uno de sus trabajos, aunque posiblemente uno de los más importantes: el teorema de Eskin–Mirzakhani–Mohammadi [7] sobre las órbitas cerradas de las superficies de traslación.
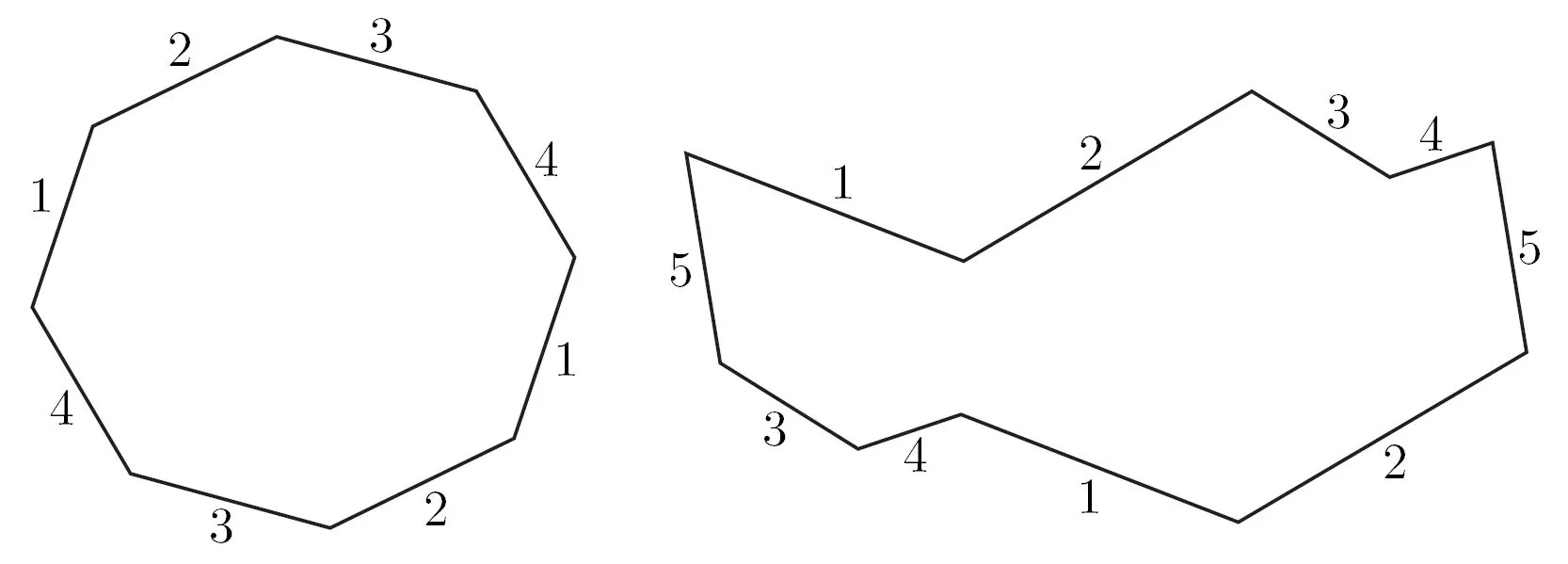
Una superficie de traslación es un polígono con las siguientes características:
1.
Tiene una cantidad par de lados.
2.
Todo lado está emparejado con otro lado opuesto, paralelo y de exactamente el mismo largo.
Ejemplos de superficies de traslación. Los números indican la forma emparejar los lados.
Ejemplos de superficies de traslación. Los números indican la forma emparejar los lados.
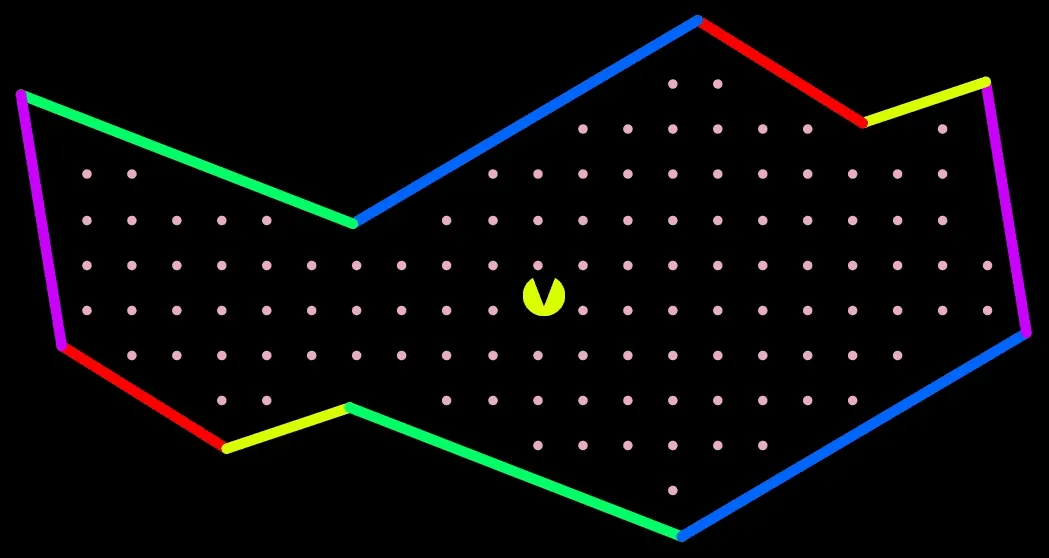
El emparejamiento de lados en realidad indica una forma de identificar los lados (en el sentido de considerarlos el mismo). Para entender mejor esta idea, recuerde cómo en Pacman el personaje aparece por el lado opuesto al salir del escenario. Nosotros proponemos una versión un poco más complicada:
Juego de Pacman en una superficie plana. Al salir del polígono se «transporta», mediante una traslación, al lugar correspondiente del lado emparejado.
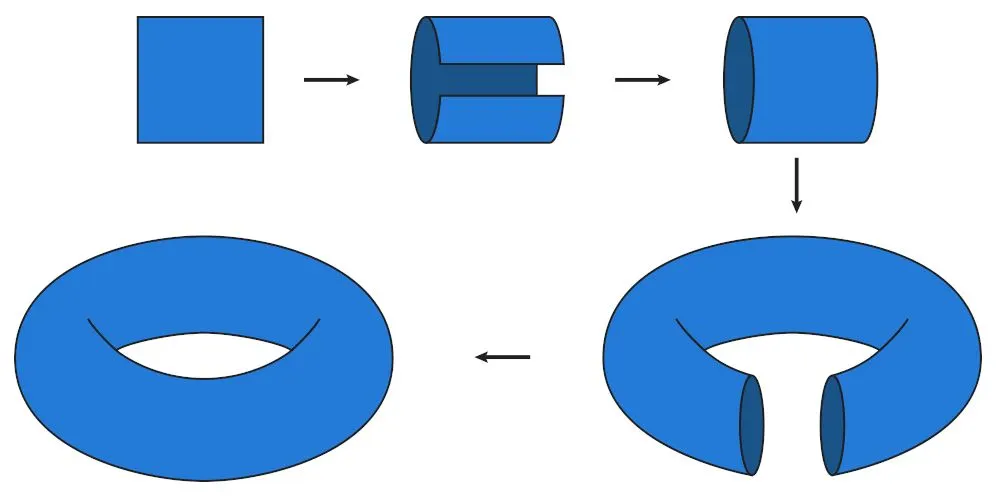
Estos objetos matemáticos se llaman superficies porque, aunque no lo parezca a primera vista, en realidad representan donas con posiblemente más de un agujero. En efecto, la idea de identificar lados del polígono también puede entenderse como pegarlos con pegamento. Siguiendo esta idea, el caso más simple de visualizar es el de un rectángulo: pegando los lados opuestos, se obtiene una dona:
Pasos intermedios al pegar los lados opuestos de un cuadrado hasta obtener una dona.
Los polígonos más complicados también producen superficies de este estilo, aunque en casos distintos al del toro es difícil visualizar los pasos intermedios. Sea cual sea el polígono inicial, se obtendrá una dona con alguna cantidad finita de agujeros.
Superficies con dos y tres agujeros. Fuente: Wikipedia.
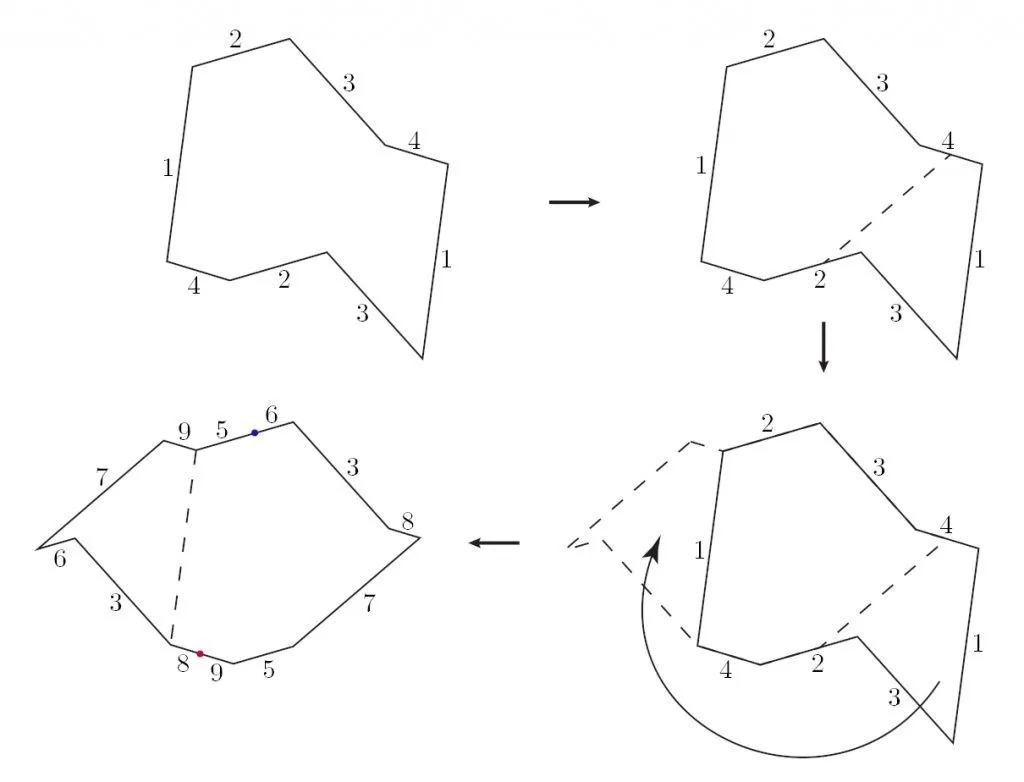
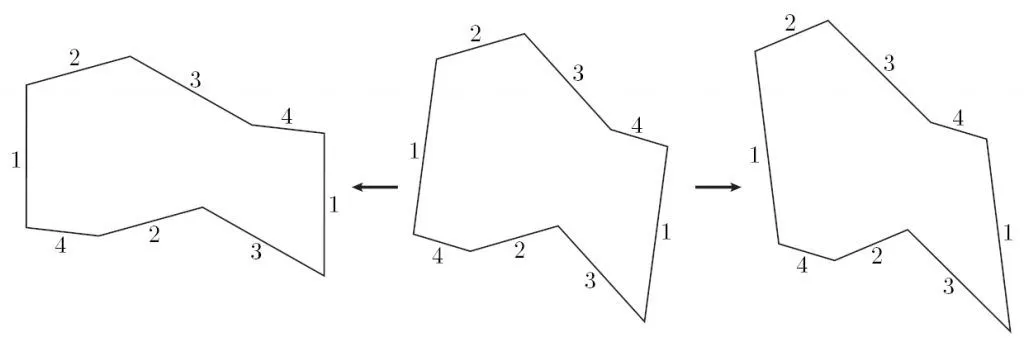
Una observación fundamental en la teoría de superficies de traslación es que éstas no cambian al aplicar operaciones de cortar y pegar. Esto es, si se corta el polígono a lo largo de cualquier línea recta y luego se pegan los trozos según los lados identificados, se obtiene exactamente la misma superficie de traslación. De hecho, como los lados del polígono fueron identificados de a pares, un polígono es solo una de muchas posibles representaciones de la superficie. Al cortar por líneas rectas y luego pegar se obtienen más formas de dibujar la misma superficie.
Comenzando con el polígono de arriba a la izquierda, elegimos una línea por donde cortar. Luego, pegamos los dos polígonos resultantes juntando sus lados 1, obteniendo finalmente el polígono de abajo a la izquierda. El polígono original y final representan exactamente la misma superficie de traslación. Note que se crearon nuevos lados etiquetados por 5, 6, 7, 8 y 9. Los dos primeros provienen de cortar el lado 2, el lado 7 proviene de la línea por donde elegimos cortar y los últimos dos de cortar el lado 4.
Comenzando con el polígono de arriba a la izquierda, elegimos una línea por donde cortar. Luego, pegamos los dos polígonos resultantes juntando sus lados 1, obteniendo finalmente el polígono de abajo a la izquierda. El polígono original y final representan exactamente la misma superficie de traslación. Note que se crearon nuevos lados etiquetados por 5, 6, 7, 8 y 9. Los dos primeros provienen de cortar el lado 2, el lado 7 proviene de la línea por donde elegimos cortar y los últimos dos de cortar el lado 4.
Además, las superficies de traslación se pueden deformar aplicando escalamientos, rotaciones y cizalladuras. Estas deformaciones dan origen, en general, a superficies de traslación distintas a la original.
Deformaciones de superficies de traslación. Note que no cambia la «esencia» del polígono: sigue teniendo la misma cantidad de lados y el emparejamiento sigue siendo el mismo.
Deformaciones de superficies de traslación. Note que no cambia la «esencia» del polígono: sigue teniendo la misma cantidad de lados y el emparejamiento sigue siendo el mismo.
Mirzakhani estudió en detalle el universo (o espacio) de todas las superficies de traslación. La observación anterior sobre los cortes por líneas rectas, sumada a la posibilidad de deformar las superficies, dota a este espacio de una rica estructura geométrica. Cerca de una superficie de traslación fija, la geometría se puede entender en términos de los lados del polígono: en efecto, cada lado se puede interpretar como un vector dotado de largo, dirección y sentido y las deformaciones corresponden a modificar linealmente estos vectores. Esto nos permite entender la geometría localmente. Sin embargo, la estructura global del espacio de las superficies de traslación es verdaderamente misteriosa y complicada.
Si consideramos todas las deformaciones posibles de una superficie de traslación dada , obtenemos su órbita. Luego, agregamos también las superficies de traslación que quedan arbitrariamente cerca de la órbita, obteniendo la órbita cerrada de . Una pregunta natural, entonces, es qué tan complicadas pueden ser las órbitas cerradas de una superficie de traslación dada. Como el espacio de las superficies de traslación es misterioso, es esperable que las órbitas cerradas sean conjuntos complicados. Lo que ella obtuvo junto a sus colaboradores es precisamente lo contrario: la órbita cerrada de cualquier superficie de traslación se puede entender, localmente, como un sistema de ecuaciones lineales (los mismos sistemas de ecuaciones que se resuelven durante la enseñanza media) donde las incógnitas son los lados del polígono.
Este resultado es sorprendente, elegante y tiene consecuencias muy fuertes en la teoría de superficies de traslación. Uno de sus principales usos es permitirnos encontrar teoremas para toda superficie de traslación en vez de para casi toda. En efecto, la mayoría de los métodos en sistemas dinámicos permiten saber qué ocurre para la mayoría del sistema, pero muy pocas veces tenemos información sobre su totalidad. En términos más concretos, los métodos en sistemas dinámicos permiten, por ejemplo, saber cómo se comportan las trayectorias de la gran mayoría de los planetas, pero si a uno le interesa saber el comportamiento de la Tierra estos métodos se vuelven, en general, inútiles. El teorema de Eskin–Mirzakhani–Mohammadi funciona como una «varita mágica» que permite pasar de lo típico a lo absoluto. De hecho, el matemático Alex Wright, luego de pasar meses entendiendo el gigantesco artículo de 172 páginas, describe este avance como «el comienzo de una nueva era. Es como si antes hubiésemos estado tratando de talar un bosque de secoyas con un hacha de mano y que ahora inventaran una motosierra» [6].
Además, el teorema tiene alcances más allá de la matemática. Por ejemplo, el espacio de las superficies de Riemann, que está íntimamente relacionado con el espacio de las superficies de traslación, da origen al espacio de las variedades de Calabi–Yau, objeto de constante estudio en física teórica.
Su legado
Mirzakhani se reconocía a sí misma como una persona que trabajaba de manera lenta. Sin embargo, su manera de trabajar fue siempre perseverante, atacando sin temor problemas difíciles y desafiantes. «Hay que ignorar la fruta más fácil de alcanzar en el árbol, lo que puede ser un poco complicado. No sé si es la mejor manera de trabajar, el camino puede parecer una tortura. Pero la vida no está hecha para que sea fácil» [4].
Siempre fue reconocida por sus pares como una persona muy talentosa, entusiasta y perseverante. «Todas las charlas suyas en la que he estado presente han estado llenas de entusiasmo chispeante y contagioso, optimismo, y una apreciación de la belleza en las matemáticas. Te inspiran a atacar problemas que parecen aterradoramente difíciles y, siguiendo los pasos de Maryam, a no darse por vencido cuando estos problemas se resisten en ser resueltos» [5].
Ser la primera mujer en obtener una medalla Fields la convirtió en una especie de símbolo en una disciplina donde el imbalance de género históricamente ha sido muy marcado. Al obtener la medalla Fields, el profesor Dame Frances Kirwan (de la Universidad de Oxford, miembro del comité de selección) dijo «espero que este premio inspire a muchas más mujeres y niñas, en este país y en todo el mundo, a creer en sus propias habilidades y soñar con ser las medallistas Fields del futuro» [2]. A pesar de no querer cargar con la responsabilidad de ser «la representante de las mujeres en las matemáticas», Mirzakhani se sentía segura de que habrían más mujeres ganadoras de medallas Fields en el futuro [4].
En una entrevista de 2004, le preguntaron qué consejo le daría a la gente que quiere saber más sobre matemáticas. «No creo que todas las personas del mundo deban convertirse en matemáticos, pero creo que muchos estudiantes no le dan a la matemática la oportunidad que se merece. Durante un par de años durante mi enseñanza básica mis notas en matemáticas fueron muy malas, simplemente porque no me interesaba pensar en ellas. Puedo entender que la matemática puede parecer fría o sin sentido si no estás interesado en ella. La belleza de la matemática solo se muestra a sus seguidores más pacientes» [3].
En el mundo científico, dominado por hombres y con desarrollo científico más bien occidental, Maryam Mirzakhani rompió estigmas y empujó la frontera del conocimiento más allá de lo que podemos actualmente vislumbrar. Su temprana partida es una gran pérdida para las matemáticas y para la ciencia mundial.
Agradecimientos
Agradecemos a Anton Zorich por las indicaciones a material bibliográfico sobre la vida y obra de Maryam Mirzakhani.
Referencias
1.
International Mathematical Union. The Work of Maryam Mirzakhani [Internet]. 2014. Disponible en: http://www.mathunion.org
2.
Maryam Mirzakhani, first woman to win maths’ Fields Medal, dies. BBC News [Internet]. 15 de julio de 2017 [citado 15 de julio de 2017]; Disponible en: http://www.bbc.com
3.
Maryam Mirzakhani: “The more I spent time on maths, the more excited I got” | Science | The Guardian [Internet]. [citado 15 de julio de 2017]. Disponible en: https://www.theguardian.com
4.
Maryam Mirzakhani Is First Woman Fields Medalist | Quanta Magazine [Internet]. [citado 15 de julio de 2017]. Disponible en: https://www.quantamagazine.org
5.
Zorich A. The Magic Wand Theorem of A. Eskin and M. Mirzakhani. arXiv:150205654 [math] [Internet]. 19 de febrero de 2015; Disponible en: http://arxiv.org
6.
Meet the First Woman to Win Math’s Most Prestigious Prize | WIRED [Internet]. [citado 15 de julio de 2017]. Disponible en: https://www.wired.com
7.
Eskin A., Mirzakhani M., Mohammadi A. Isolation, equidistribution, and orbit closures for the action on moduli space. Annals of Mathematics. 1 de septiembre de 2015;673–721.