Las recientes elecciones de parlamentarios y consejeros regionales utilizaron un «nuevo» sistema en reemplazo del sistema binominal. Ya dedicamos un artículo a explicar cómo funciona este nuevo sistema y la motivación detrás de los sistemas electorales «proporcionales» en general, por lo que supondremos que usted los conoce.
Este cambio produjo algunos resultados controversiales en la elección recién pasada. En particular, la prensa destacó los siguientes casos:
1.
El candidato a senador más votado en la Circunscripción 1 de Arica y Parinacota, Enrique Lee Flores, no fue electo.
2.
La amplia votación obtenida por el reelecto diputado Giorgio Jackson en el Distrito 10 de La Granja, Macul, Ñuñoa, Providencia, San Joaquín y Santiago provocó que algunos de sus correligionarios de Revolución Democrática fueran electos, a pesar de que el porcentaje de votos individuales que obtuvieron fue cercano al 1%.
3.
Florcita «Motuda» Alarcón resultó electo diputado en el Distrito 17 tras obtener el 2,38% de los votos en total, siendo superado por candidatos de otras listas que no fueron electos. Esto lo llevó a decir que el sistema «no era democrático». Y que más democrático que elegir una Florcita (?).
En este artículo no queremos centrarnos en estos casos polémicos particulares, sino más bien estudiar en general el «sistema proporcional» y cómo se compara con otros sistemas existentes. ¿Por qué el sistema reparte los escaños de esa forma? ¿Cómo medimos si el sistema es bueno o es malo? ¿Se puede modificar el sistema para que los casos polémicos no sucedan?
Si bien ya explicamos el razonamiento tras el método D’Hondt y el «sistema nuevo», ahora con los resultados en mano podemos comparar cómo funcionó el sistema con respecto a otros sistemas existentes, incluido el binominal. Para ello usamos los votos de esta elección y estudiamos los resultados bajo distintos sistemas de distritaje y de asignación de escaños. Luego, comparamos los métodos usando índices ampliamente citados en la literatura para medir que tan «buenos» son los resultados obtenidos. Finalmente, contrastamos los resultados de nuestro análisis con otros diagnósticos que se han hecho al nuevo sistema.
¿Cómo medimos si un método es mejor que otro?
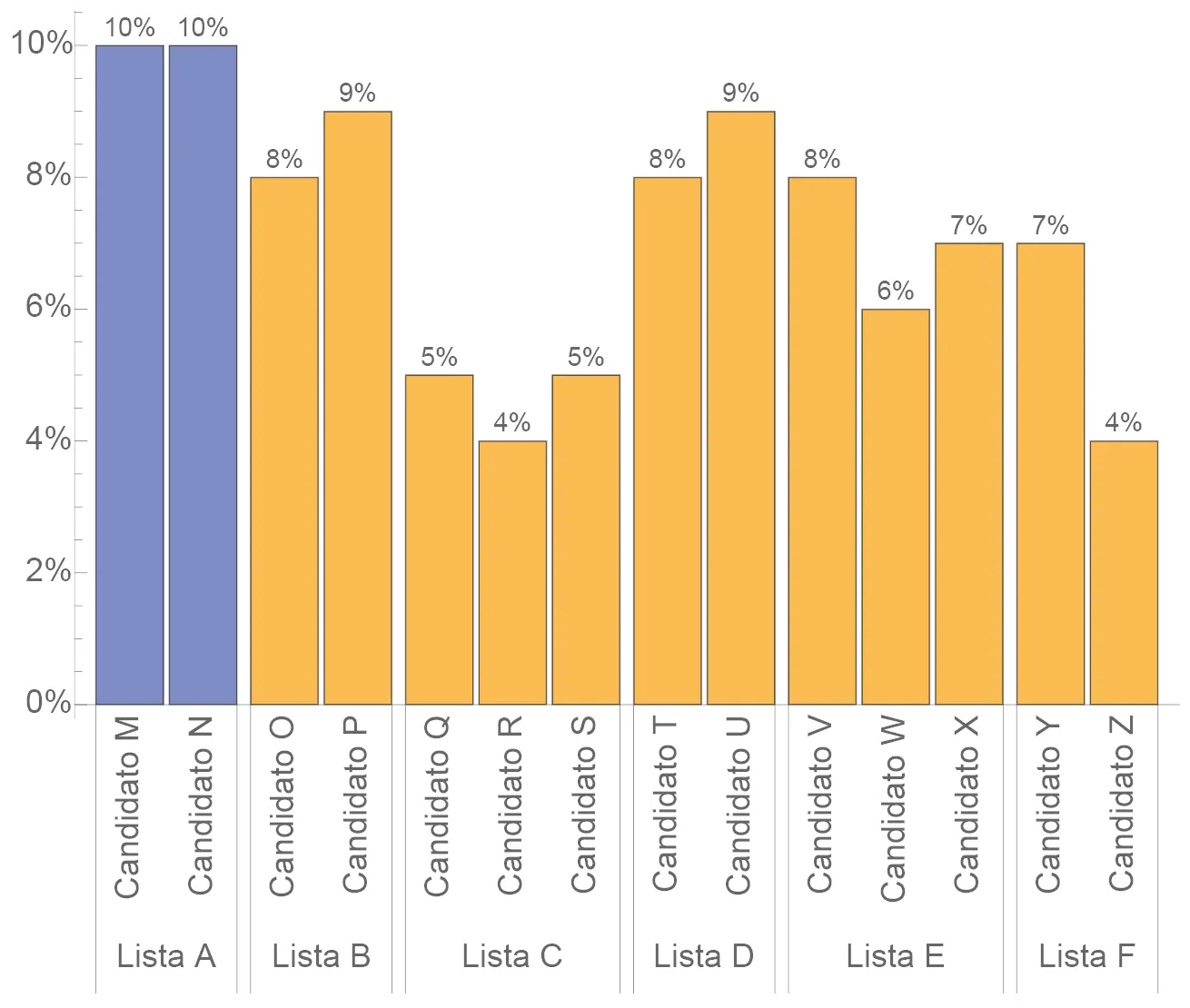
El método D’Hondt está pensado para que los puestos obtenidos por cada coalición y partido sean lo más cercanos posible a los votos obtenidos, como se explicó anteriormente. Si bien ya se discutió el porqué, podemos dar un ejemplo que puede ayudar a entender por qué un método como seleccionar «los más votados» en cada división electoral puede generar problemas. Digamos que se eligen exactamente dos candidatos en cada distrito: existe una Lista A que tiene el 20% de los votos en total, cuyos dos candidatos obtienen 10% y 10% de los votos respectivamente (lo que no es tan extraño si participan, digamos, más de diez candidatos en cada distrito). El resto de los candidatos de otras listas obtienen menos de 10% cada uno. Si elegimos los dos candidatos más votados en cada distrito, la Lista A se lleva el 100% de los puestos en el parlamento... ¡pero sólo tiene el 20% de los votos!
En este ejemplo, elegir «los más votados» genera dos distorsiones. 1) Los candidatos M y N serían electos, a pesar que la lista E obtiene más porcentaje de votos que la Lista A. 2) Lista A obtiene el 100% de los candidatos con sólo el 20% de los votos. Si esta situación se replica en todos los distritos, los escaños totales en el parlamento no estarán bien distribuídos de acuerdo a los votos.
En este ejemplo, elegir «los más votados» genera dos distorsiones. 1) Los candidatos M y N serían electos, a pesar que la lista E obtiene más porcentaje de votos que la Lista A. 2) Lista A obtiene el 100% de los candidatos con sólo el 20% de los votos. Si esta situación se replica en todos los distritos, los escaños totales en el parlamento no estarán bien distribuídos de acuerdo a los votos.
Resulta evidente que el ejemplo de juguete es artificial y poco realista. En el caso de una elección real, no es tan claro, a priori, que una asignación de escaños sea mejor que otra. Por ejemplo, en el Distrito 10 Revolución Democrática obtuvo el 25,89% de los votos. Con el método proporcional de D’Hondt, terminó obteniendo el 37,5% de los escaños del Distrito, por lo que está sobrerrepresentado. Si se hubiesen elegido, en cambio, a los candidatos que obtuvieron más votos individuales, tendría sólo el 12,5% de los escaños y estaría subrepresentado. Este ejemplo muestra que es necesario buscar formas más globales de poner a prueba un método, que no sólo consideren lo que pase con una o unas pocas listas sino con la elección completa.
Entendido esto, se fija que la óptica usada para medir lo bueno de un método de elección es mediante cuánto se parecen los porcentajes obtenidos por partido-pacto a los porcentajes obtenidos en los votos. Por supuesto, esto deja fuera muchas dimensiones en las que es posible evaluar un método electoral, pero nos centraremos en esta porque responde a la buscada «teóricamente» por los sistemas proporcionales. Recordemos que, por la manera en que está diseñado, el «nuevo sistema proporcional» debería ser mejor que el binominal en este sentido. Sin embargo, estudios realizados pocos días después de las elecciones de noviembre concluían que el nuevo sistema funcionaba peor que la distribución lograda en elecciones anteriores, donde se usó binominal (1,5).
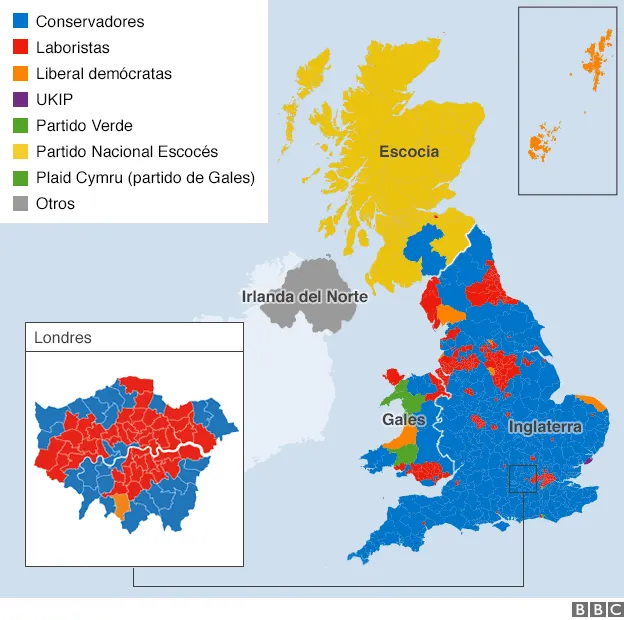
¿Cómo medimos qué tan cerca está un modelo de acercarse a la distribución perfecta entre votos y escaños obtenidos? Los cientistas sociales han «inventado» muchas maneras (no todas comparables) de medir la distancia entre el porcentaje de votos y el porcentaje de escaños obtenido por partidos, dando lugar a distintos índices para evaluar lo «bueno» de un sistema de elección (3,4). Cada uno de estos índices entrega un número: mientras más bajo sea, mejor es el método. Sin embargo, estos índices no capturan el hecho de que las coaliciones y la sociedad se adaptan a los sistemas de elección: el sistema binominal favorecía la subsistencia de dos coaliciones grandes y desincentivaba el resto, y esto se veía reflejado en el relativo bajo protagonismo y participación de candidaturas alternativas. A su vez, la existencia o no de dos coaliciones grandes afecta al cálculo de desproporcionalidad independiente del sistema de repartición utilizado. Un ejemplo donde esta distribución de votos se refleja en la desproporcionalidad es el caso británico: los índices de desproporcionalidad subieron cuando se comenzó a romper el duopolio laborista-conservador a pesar de que no se cambió el método de votación (6). [Prometemos no volver a decir desproporcionalidad]
Resultados de una elección general (parlamentaria) en Reino Unido. Note la ausencia de duopolio.
Resultados de una elección general (parlamentaria) en Reino Unido. Note la ausencia de duopolio.
En la misma línea, en la literatura se mencionan diversos efectos que no dependen del método de repartición que afectan la proporcionalidad: la distribución de votos en las listas, la cantidad de escaños por distrito, o si existen distritos donde se asigne una cantidad mayor de escaños per cápita que en otras (4). Otro detalle, más básico aún y que dificulta la comparación, es que la forma en que estos índices están definidos los hace muy sensibles a factores como la cantidad total de pactos en cada elección.
Cabe decir que todos los puntos mencionados anteriormente han variado muchísimo entre las elecciones parlamentarias chilenas realizadas desde 1989 a la fecha. Dado esto, resulta evidente que estos índices no permiten comparar de manera conclusiva elecciones distintas, sino sólo distintos métodos aplicados a la misma elección.
Por eso en nuestro análisis decidimos usar distintos métodos para decidir quiénes resultan electos a los datos de votos la elección parlamentaria de noviembre de 2017 y 2013. Luego, comparamos estos método usando los índices mencionados anteriormente. Los datos fueron obtenidos de la página del Servel. Al final del artículo presentamos un repositorio con los datos que usamos y el resultado de nuestros cálculos.
Todos los métodos, una voz
Decidimos estudiar once métodos distintos de asignación de escaños, todos con los votos obtenidos en las elecciones de diputados del 19 de noviembre de 2017. Los métodos usan distintos sistemas de asignación de escaños o distintos distritajes (división electoral del país), pero siempre los mismos votos y pactos de esta elección.
Unas aclaraciones antes de explicar los métodos estudiados.
1.
Primero, el método de Sainte-Laguë es similar al método D’Hondt (explicado en nuestro artículo anterior) pero ahora los números por los que se «dividen los resultados» son más altos. Recuerde que en el método D’Hondt el total de votos obtenidos por un pacto o partido se divide por 1, 2, 3, 4 y así sucesivamente. En el método de Sainte-Laguë, la tabla se completa dividiendo por 1, 3, 5, 7 y así sucesivamente. Es decir, se usan los números impares. El objetivo detrás de esto es establecer una leve preferencia a los pactos o partidos que obtienen menos votos en cada elección.
2.
Segundo, decidimos estudiar separadamente los sistemas aplicados para asignar los cupos a cada pacto y luego a cada partido. El sistema actual usa D’Hondt en ambos casos, lo que da a lugar a situaciones contraintuitivas (como el caso del Distrito 10 explicado anteriormente). Esta distinción importa si es que las personas tienen preferencias amplias por un pacto pero más personalizadas dentro de cada pacto.
3.
Tercero, analizamos el caso de un solo distrito a nivel nacional donde se eligen la totalidad de los candidatos. No es tan pelacables como suena: es el sistema ocupado en Países Bajos (por ejemplo) y teóricamente debería entregar la «mejor repartición» posible entre votos obtenidos y el total de los escaños, pues son los distritos chicos los que más distorsionan los resultados.
Sin más preámbulos, estos son los modelos estudiados.
1.
Usando el distritaje nuevo:
a.
Doble D’Hondt: se usan dos rondas de método D’Hondt; primero para asignar los cupos a cada pacto y luego para asignar los cupos a cada partido. Este método fue el usado oficialmente en esta elección.
b.
Sólo «los más votados»: se asignan siempre los escaños a los candidatos más votados, sin consideración ni de pacto ni partido.
c.
D’Hondt y «los más votados»: se usa D’Hondt para asignar los cupos a cada pacto y dentro de cada pacto se asignan los escaños sólo considerando los más votados (sin consideración de pertenencia a partidos).
d.
Doble Sainte-Laguë: se usan dos rondas de Sainte-Laguë, primero para asignar cupos a cada pacto y luego para asignar cupos a cada partido.
e.
D'Hondt y Sainte-Laguë: se usa una ronda de D’Hondt para asignar cupos a cada pacto y luego una ronda de Sainte-Laguë para asignar cupos a cada partido.
f.
Sainte-Laguë y «los más votados»: se usa Sainte-Laguë para asignar los cupos a cada pacto y dentro de cada pacto se asignan los escaños sólo considerando los más votados (sin consideración de pertenencia a partidos).
2.
Usando el distritaje antiguo:
7. Binominal a la antigua: asignando dos escaños a cada distrito, se usa el sistema binominal con los votos obtenidos ahora.
8. Binominal y «los más votados»: asignando dos escaños a cada distrito, seleccionamos en cada uno los dos candidatos más votados.
3.
Usando un único distrito a nivel país, combinando todos los votos:
9. Todos contra todos y D'Hondt: se asigna el total de los escaños ocupando D’Hondt en pactos y partidos.
10. Todos contra todos y «los más votados»: se asigna el total de los escaños seleccionando sólo a los candidatos más votados.
11. Todos contra todos y Sainte-Laguë: se asigna el total de los escaños ocupando Sainte-Laguë en pactos y partidos.
Resultados
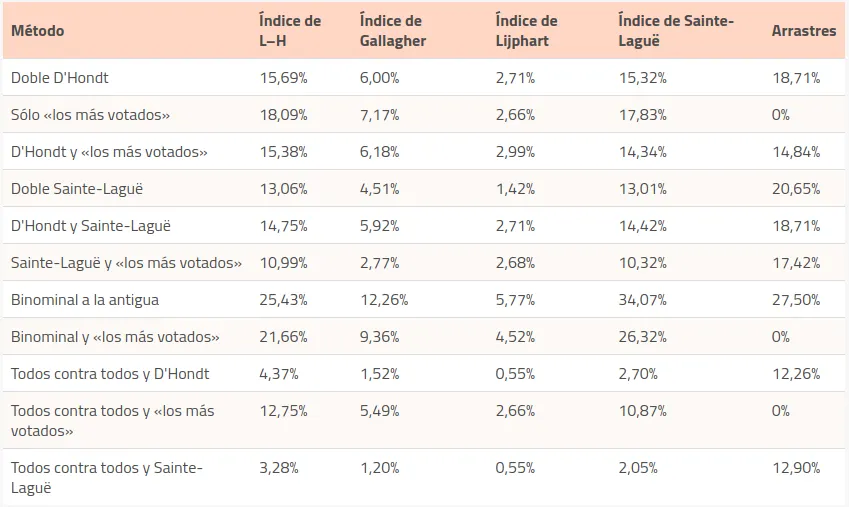
Ahora que tiene una idea de cómo funcionan estos métodos, podemos presentar los resultados a nivel país. Le recordamos que el resultado «ideal» de la votación es que los porcentajes de candidatos electos pertenecientes a un pacto o partido se parezcan mucho a los porcentajes de votos obtenidos por tal pacto o partido. Así, si un partido obtiene el 30% de los votos a nivel nacional, nos gustaría que el 30% de los candidatos electos pertenecieran a tal partido. Como ya le adelantamos, existen muchos «índices» que miden la distancia entre el resultado ideal y el resultado para un método particular, con amplio uso en la literatura. En este artículo privilegiamos cuatro de estos índices.
El índice de Loosemore–Hanby tradicionalmente ha sido el más usado para medir la desproporcionalidad [ok, mentimos, teníamos que decir «desproporcionalidad» algunas veces más], no sin críticas: funciona mejor en algunos métodos sobre otros y no mide bien escaños que están repartidos entre partidos subrepresentados (4,6). Para eso se ha propuesto el uso de los otros índices que usamos, los de Gallagher, Lijphart y Sainte-Laguë.
Además, mostramos el porcentaje de candidatos que fueron electos a pesar de que no estuvieron entre los más votados, lo que llamamos «arrastres».
Si bien los métodos se ordenan de forma distinta de acuerdo al índice usado, se aprecia una tendencia más o menos clara: los métodos que usan el binominal son más desproporcionales que el resto de los métodos, los métodos que usan un solo distrito son los más proporcionales de todos y el método usando el distritaje actual está en un punto intermedio.
Dentro de los métodos que usan el distritaje actual, el método usando D’Hondt dos veces (lo que se usa actualmente) es uno de los más proporcionales, sólo mejorado por el que usa el método de Sainte-Laguë dos veces. En general, usar «los más votados» aumenta la desproporcionalidad, pero, en contraste, el método de usar D’Hondt entre pactos y luego los más votados dentro de cada pacto es comparable al método actual. El método binominal es, por lejos, el más desproporcional usando los datos actuales.
Además, hicimos un análisis similar con los datos de la elección parlamentaria de noviembre de 2013. En este caso, el sistema binominal con el distritaje antiguo (sistema 6) funcionaba ligeramente mejor que el nuevo sistema proporcional (sistema 1) según estos cuatro índices.
Discusión
Con datos en mano podemos discutir alrededor de algunos informes hechos evaluando el sistema actual. Una nota publicada por David Altman (1) compara la proporcionalidad entre las elecciones parlamentarias de 1989 a la fecha usando el índice de L–H y concluye, incluso formando parte de su título, que el nuevo sistema es menos proporcional y más injusto. Como fue discutido anteriormente, muchísimos factores afectan la proporcionalidad aparte del sistema de votación, por lo que la comparación entre elecciones de años distintas es, al menos, insuficiente para realizar una afirmación tan tajante. Además usa sólo el índice de L–H para medir la proporcionalidad, pero como fue dicho anteriormente, se han presentado observaciones sobre el uso exclusivo de este índice (4, 6).
En un artículo en La Situación, Andrés Hernando y Javier Sajuria (2) matizan el análisis anterior y realizan la comparación entre elecciones parlamentarias de distintos años usando ocho índices distintos, donde en algunos el nuevo sistema resulta favorecido y en algunos no. Usan esto para argumentar que la elección no se debe medir sólo en términos de proporcionalidad usando los índices sino que debe considerarse cómo el nuevo sistema mejora en términos de representatividad, considerando conceptos como promedio de edad de las nuevas bancadas, porcentaje de mujeres, la diversidad de partidos que ahora forman parte de las cámaras, etc. Consideramos esto como un punto de vista válido, pero alejado de lo que podemos medir sólo con los datos que tenemos.
En un boletín de Libertad y Desarrollo (5), dado a conocer el 3 de diciembre en El Mercurio, se hace el mismo análisis realizado por Altman (usando el índice de L–H); además de la simulación de cómo habría resultado la distribución de escaños con los votos actuales si se hubiese usado el binominal (correspondiente al método de «Binominal a la antigua» en nuestras simulaciones). Con esto, concluyen que la proporcionalidad hoy es menor a la obtenida con el sistema binominal en elecciones anteriores. Además afirman (aunque sin mencionar cálculos) que al eliminar que los partidos actúen como subpactos a nivel de listas se eliminarían «distorsiones». El estudio presenta muchos problemas, partiendo porque los datos que presentan son incorrectos (muestran, por ejemplo, que con el método actual Chile Vamos obtuvo 73 diputados y los «regionalistas, independientes y otros» tienen 5 escaños, pero los números reales son 72 y 6 respectivamente). El segundo problema es la afirmación tajante de que el nuevo sistema «disminuye la proporcionalidad» cuando, por las razones esgrimidas anteriormente, no son comparables directamente, menos mediante el uso de un solo índice. Además, nuestro análisis muestra que el porcentaje de «arrastres» es mayor con el sistema binominal. Por último, a pesar de que realizan la simulación con los votos actuales aplicando el binominal —obteniendo resultados muy similares a los nuestros—, omiten el cálculo de la desproporcionalidad obtenida usando ese sistema (25,43% en índice L–H). Como vimos en los resultados, esto es bastante peor que lo obtenido con el sistema actual (15,69% en índice L–H).
Conclusiones
Para la elección de noviembre de 2013, el sistema binominal era más proporcional que el sistema nuevo, aunque la diferencia es bastante menor a la que se observa en la elección de 2017. Inferimos que el sistema binominal funcionaba relativamente bien porque existían dos grandes coaliciones, cada una de las cuales obtenía aproximadamente la mitad de los votos. Se fomentaba una situación duopólica, incentivando la homogeneidad de opiniones dentro de cada coalición y, por lo tanto, coartando la representatividad. El escenario político chileno ha cambiado, siendo ahora más complejo y diverso. Es necesario, entonces, utilizar un método adaptado a este escenario.
Como conclusiones finales, vemos que no es trivial comparar la proporcionalidad entre elecciones de distintos años, menos aún cuando cambiaron cosas tan relevantes como el método, los distritos y las fuerzas políticas mayoritarias en disputa. Usando los datos de la elección actual y distintos modelos puede verse que el sistema actual funciona relativamente bien en estos términos, aunque no es el mejor sistema existente. El modelo de usar D’Hondt a nivel de pactos y luego «los más votados» es comparable en proporcionalidad y elimina algunos de los casos de «arrastre»; el de Sainte-Laguë a nivel de pactos y luego «los más votados» mejora bastante la proporcionalidad y también elimina «arrastres». Los métodos que minimizan los índices son los que consideran todo el país dentro de un solo distrito, pero aplicar esto en la práctica requeriría de un cambio de paradigma de acuerdo a cómo se organizan las elecciones y puede producir consecuencias no deseadas.
Archivos auxiliares
Agradecimientos
Gracias a Alfredo Cádiz por su ayuda con la obtención de los datos del Servel y a Chaparrón Bonaparte por sus valiosas sugerencias y discusión sobre métodos proporcionales.
Referencias
1.
David Altman, Nuevo Sistema Electoral: Más Flexible, Menos Proporcional y Más Injusto. (2017) Disponible acá.
2.
Andrés Hernando y Javier Sajuria. La belleza está en el ojo del que mira. O por qué esta elección no fue ni más ni menos proporcional que la anterior, pero sí más representativa. (2017) Disponible acá.
3.
Aikaterini Kalogirou y John Panaretos. Analysis and comparison of Greek parliamentary electoral systems of the period 1974-1999. (1999) Disponible acá.
4.
Michael Gallagher, Proportionality, disproportionality and electoral systems (1991) Electoral Studies Vol. 1 https://doi.org/10.1016/0261-3794(91)90004-C
5.
Libertad y Desarrollo, Evaluando el nuevo sistema electoral: expectativa y realidad. (2017) Disponible acá.
6.
Alan Renwick, Electoral Disproportionality: What Is It and How Should We Measure It? (2015) https://blogs.reading.ac.uk/readingpolitics/2015/06/29/electoral-disproportionality-what-is-it-and-how-should-we-measure-it/