Advertencia: este artículo no intenta predecir el desarrollo de la epidemia de COVID-19 en Chile. Los gráficos son solo presentados a modo de ejemplo y no usan datos reales. Si usted busca pronósticos serios, le recomendamos recurrir a los recursos oficiales y a los que han compartido expertas y expertos en modelos epidemiológicos. Aquí tiene acceso a los recursos de la Organización Mundial de la Salud (OMS) y a los de los Centros para el Control y Prevención de Enfermedades de Estados Unidos (CDC).
La gran curva
La situación mundial en abril de 2020 a causa de la pandemia del SARS-CoV-2 (más conocido como «coronavirus») es, sin duda, preocupante. Una de las dudas más recurrentes es cómo va a evolucionar la situación en el futuro. Saber esto es de vital importancia para las sociedades y los gobiernos de todo el mundo: tener una idea de cómo se propaga y cómo afecta la pandemia permite determinar dónde son necesarios los cordones sanitarios y cuarentenas, cómo relocalizar insumos, dónde deben reconvertirse camas y suspender cirugías electivas, determinar qué insumos deben comprarse y cómo reforzar los turnos del personal del salud, entre muchas otras medidas y políticas de salud pública que permitan manejar los efectos de esta pandemia.
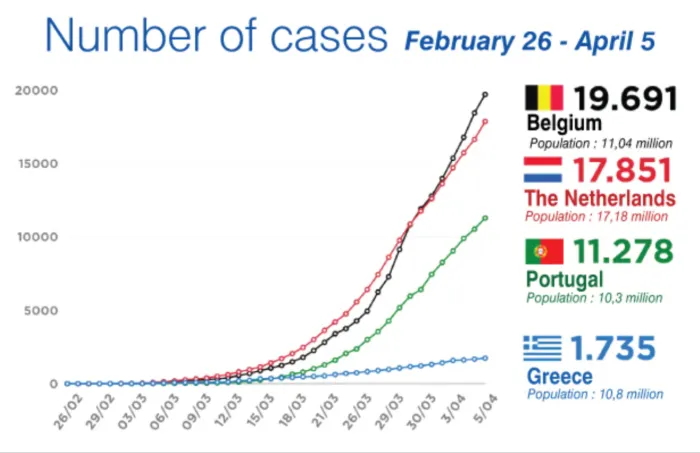
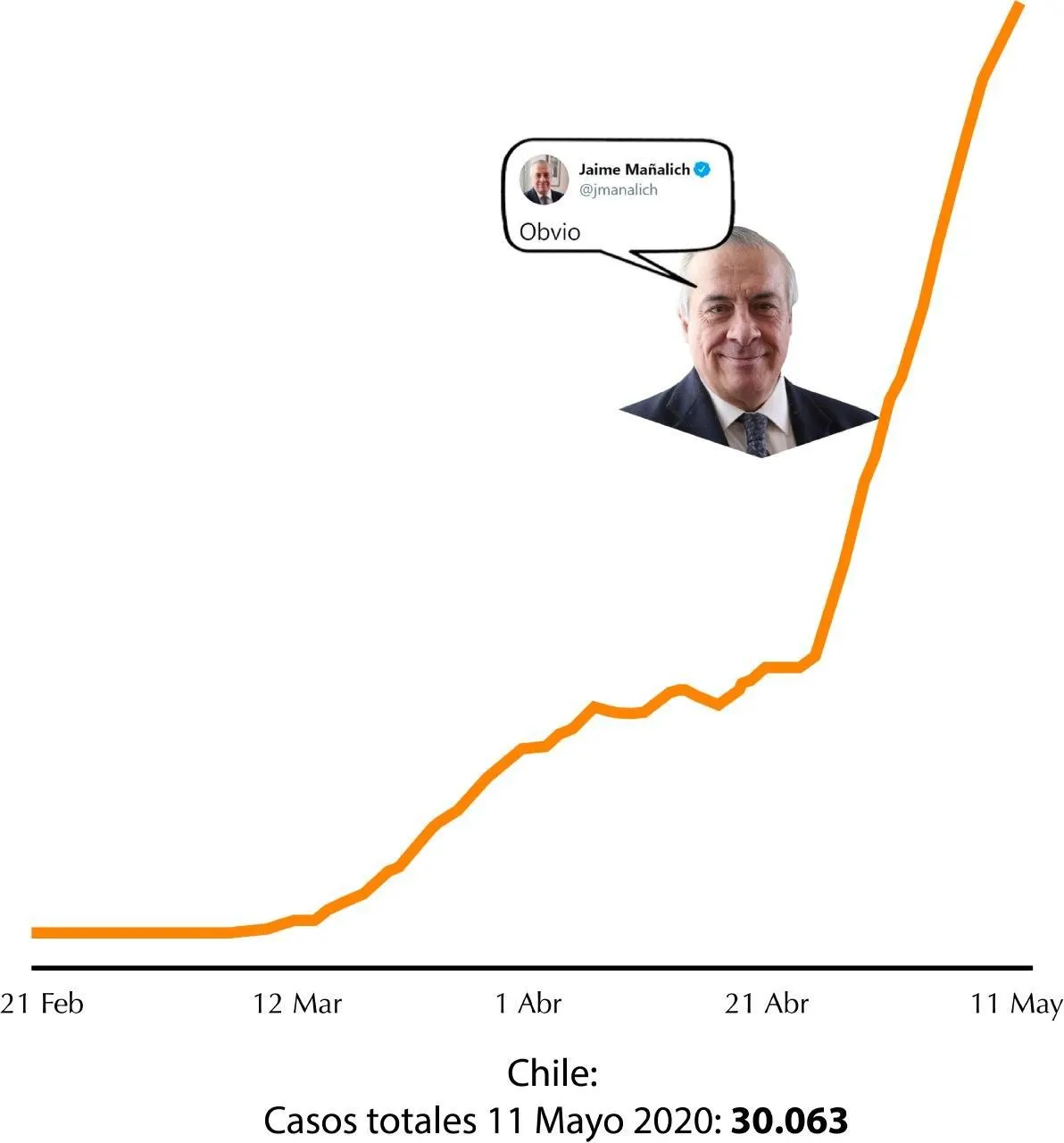
Como hay mucha incertidumbre sobre la evolución de la pandemia, muchas personas han hecho circular incontables gráficos con curvas que muestran datos como la cantidad de contagiados o muertos por día y comparaciones de estas «curvas» en distintos países. Probablemente, usted habrá visto alguno así:
Estos diagramas muestran cómo ha sido el comportamiento de los casos hasta ahora. Pero, ¿cómo podemos usar estos datos para tratar de predecir cómo estaremos en el futuro? Una primera idea sería suponer que el crecimiento sigue tal cual lo sugiere la curva... hasta el infinito.
La cosa, por supuesto, no es tan simple (pese a lo que pretendan hacerle creer los cientos de «epidemiólogos» aficionados que usted puede encontrar en Twitter). Ya sea porque la población no es infinita, porque hay personas que nunca se van a contagiar, porque algunas se van a sanar o morir sin saber nunca que tenían COVID-19 o porque faltan datos esenciales, estos gráficos no son para que los haga un ingeniero comercial en la servilleta del almuerzo.
La academia ha estudiado el tema de la modelación por mucho tiempo y ha logrado dar con modelos sofisticados que permiten entender estos fenómenos de forma mucho más certera. Nuestro objetivo ahora es presentar algunos de estos modelos para entender algunas de las consideraciones se deben tener a la hora de generar predicciones.
El famoso (y el menos famoso )
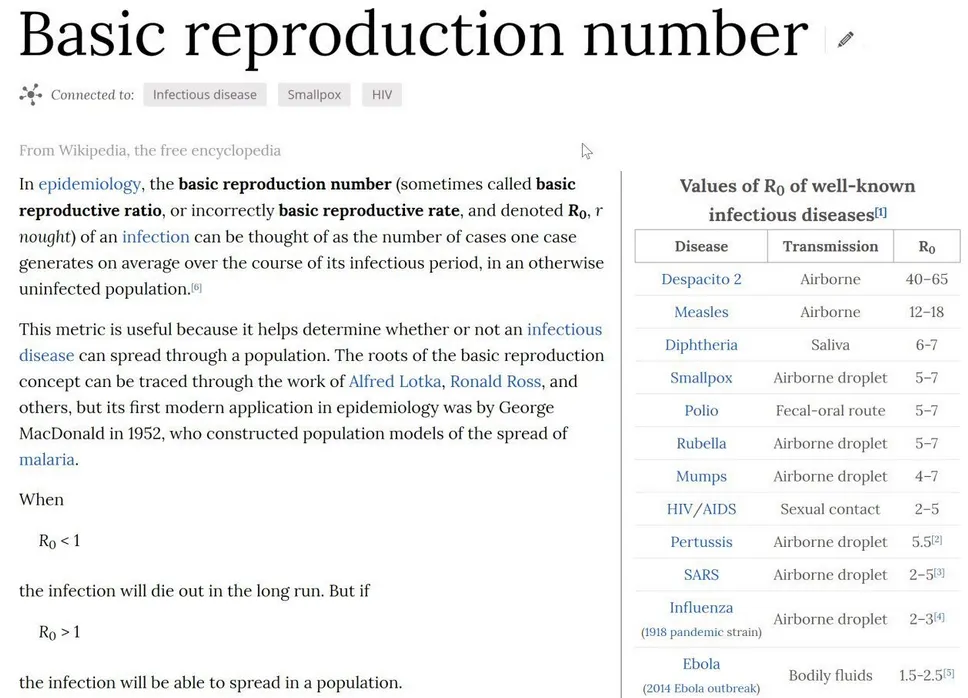
Un parámetro muy importante para entender estos modelos es el ritmo reproductivo básico, un número que se denota por . Cada enfermedad infecciosa tiene su propio valor de asociado. Muy resumidamente, el significado de este valor es el siguiente: mientras más alto es el valor de de una enfermedad, más difícil es controlarla en caso de epidemia. Y, por supuesto, mientras más bajo es dicho valor, más fácil es controlarla. Idealmente, se debe aspirar a que el no sea mayor que 1, pues esto indica que la epidemia ya no presenta aceleración en su ritmo reproductivo.
Una definición más precisa sería la siguiente: el es el número promedio de personas que una sola persona infectada va a contagiar, bajo la suposición de que todas las personas son igualmente contagiables y que no se están aplicando medidas de mitigación. Enfermedades poco contagiosas como el MERS tienen un entre 0,3 y 0,8, mientras que enfermedades muy contagiosas como el sarampión tienen un entre 12 y 18. En el caso del COVID-19, todos los resultados son muy recientes, pero por ahora se estima que su está entre 2 y 2,5 [9].
Para una población específica, el valor de de cada enfermedad se puede estimar usando datos experimentales, es decir, midiendo las variaciones en la cantidad de infectados en una población por un intervalo de tiempo. Es importante recalcar que este número no es una constante «biológica» o «intrínseca» del agente patógeno. El ritmo con el que se propaga la enfermedad depende de las características intrínsecas del bicho microscópico en cuestión, pero también de características foráneas: depende del grupo humano que se esté estudiando, de su comportamiento y posiblemente de otros factores ambientales.
Un número relacionado y similarmente importante es el ritmo reproductivo efectivo, denotado (o efectivo). A diferencia del , el se define como el número promedio de personas que una sola persona infectada va a contagiar en un instante específico del tiempo y tomando en cuenta todas las medidas de mitigación que están siendo aplicadas en ese momento. Este número puede variar en el tiempo, pues toma en consideración factores como el uso de vacunas (cuando existen), la existencia de cuarentenas, el cierre de los establecimientos educativos, etc. Tal como el , este número se puede estimar experimentalmente. En el caso de Chile, los datos hasta el 10 de mayo de 2020 sugieren un valor de de entre 1,2 y 1,5 [10].
A pesar de que y el son distintos, en los artículos no especializados muchas veces se les llama a ambos. Por esta razón, le recomendamos prestar especial atención sobre el significado de en cada artículo que lea.
Yéndose por las ramas
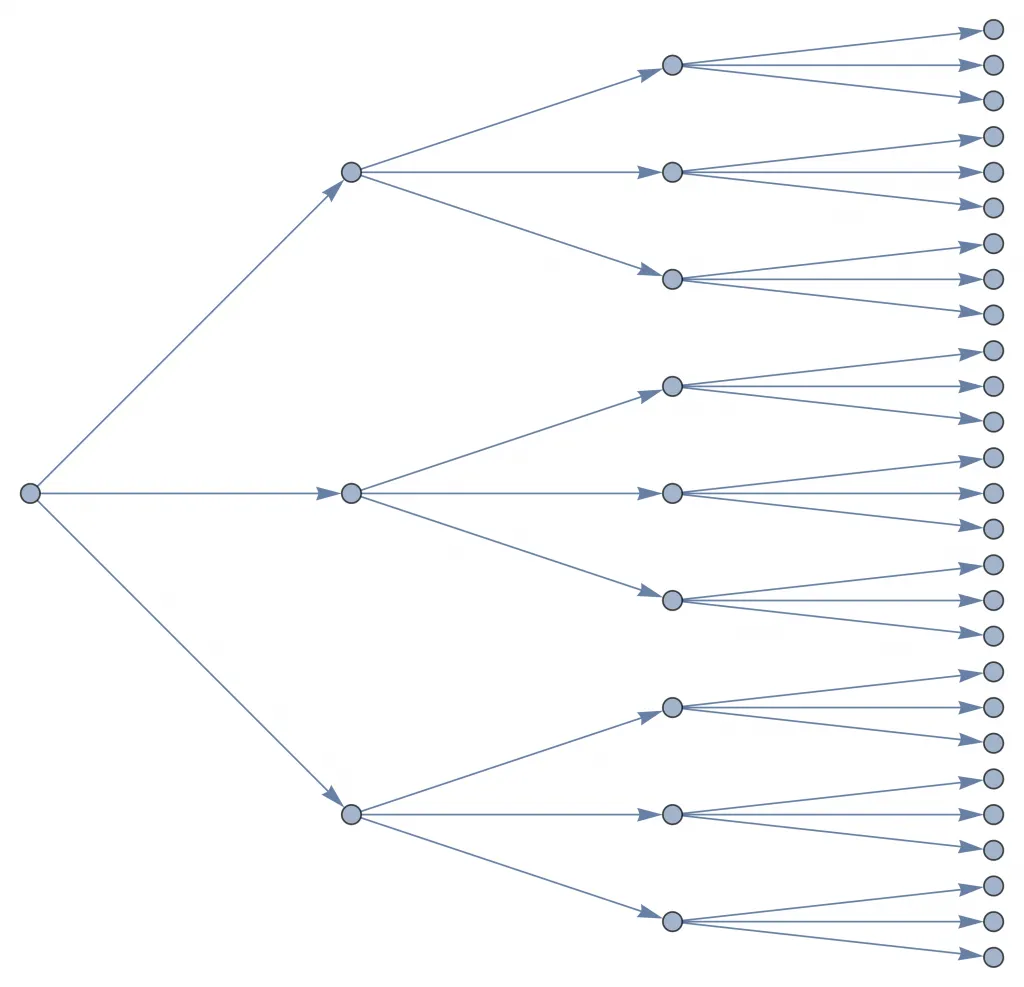
Imaginemos por un momento que todas las personas fuéramos iguales. Cada una tiene la misma cantidad de amigos y se comporta de la misma forma. Así, cada persona contagiada va a transmitir el agente patógeno de exactamente la misma manera. Además, supongamos el comportamiento de una persona es independiente del resto. Bajo estos supuestos, una persona contagiada va a contagiar a exactamente personas. Luego, cada una de estas personas personas va a contagiar a otras personas y así sucesivamente.
El primer punto a la izquierda es la primera persona infectada. En la segunda columna, se ve que contagió a tres personas. Cada una de estas contagia a tres, obteniendo nueve en la tercera columna y finalmente veintisiete en la cuarta.
El crecimiento bajo este modelo simplista es exponencial. En un modelo exponencial, la cantidad de contagiados crece «multiplicativamente» en cada intervalo de tiempo, digamos, en cada día. Por ejemplo, si y en un día había 1 infectado, bajo este modelo esperamos que en un día más haya 2 nuevos infectados, en dos días más haya 4, en tres días más haya 8, y así sucesivamente.
Este modelo es extremadamente simple, pero podemos modificarlo de a poco para obtener cosas más realistas. Como primer paso, podemos incluir el azar como un factor.
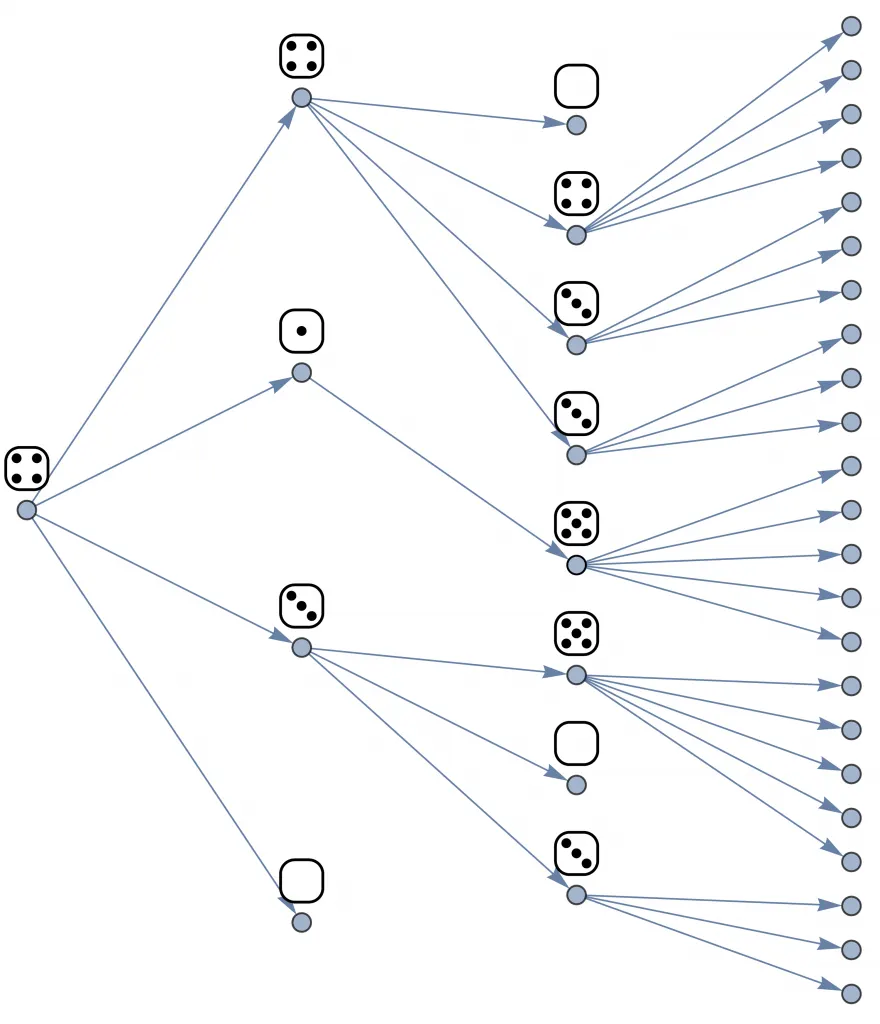
Imaginemos que cada individuo contagiado tiene un dado. Los dados de todas las personas son indistinguibles entre sí: todos tienen seis caras, números del 0 al 5 y están perfectamente balanceados (o sea, la probabilidad de que salga cada número es la misma). Ahora, un infectado va a contagiar exactamente a la cantidad de individuos que obtiene al lanzar su dado. Como todos los dados son indistinguibles entre sí, decimos que todos los contagiados van a transmitir el agente de forma idénticamente distribuida. Por otro lado, como cada persona tiene su propio dado que lanza sin influencia del resto, decimos que estas distribuciones son independientes entre sí. En este caso, el será el valor promedio que da el dado, es decir, (0+1+2+3+4+5)/6 = 2,5.
La primera persona infectada ahora transmite el agente patógeno a cuatro otras personas, porque eso dio su dado. Las siguientes, en la segunda columna, lo transmiten a cuatro, una, tres y cero. Se continúa después de la misma forma.
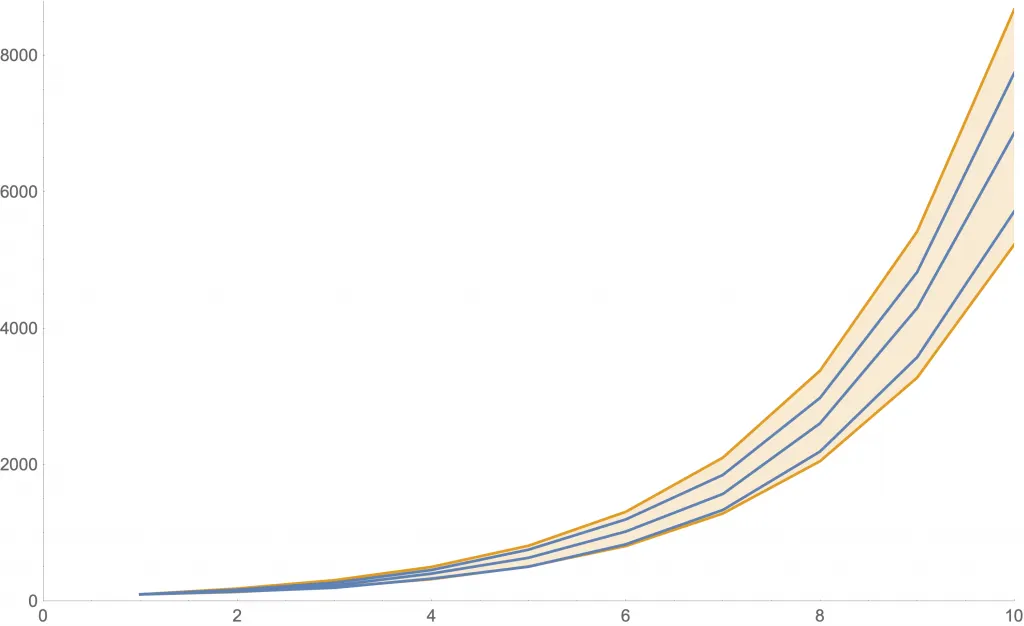
Ejemplos de la cantidad de nuevos casos con este modelo con dados. Como las curvas son aleatorias, mostramos tres de ellas en azul. Además, la zona anaranjada muestra dónde estará una curva con al menos 80% de probabilidad.
Para obtener modelos más realistas, podemos usar probabilidades de contagio más complicadas que el lanzamiento de un dado, pero que de todos modos sean independientes e idénticamente distribuidas. Esto es lo que conoce como un proceso de Bienaymé–Galton–Watson y es un tipo particular de proceso de ramificación.
El comportamiento a largo plazo de un proceso de este tipo es bastante simple: si , la enfermedad está condenada a la extinción (es decir, finalmente no habrá personas contagiadas), pero, si , se tendrá un crecimiento exponencial indefinido. Por esta razón, sigue sin ser demasiado útil en la práctica.
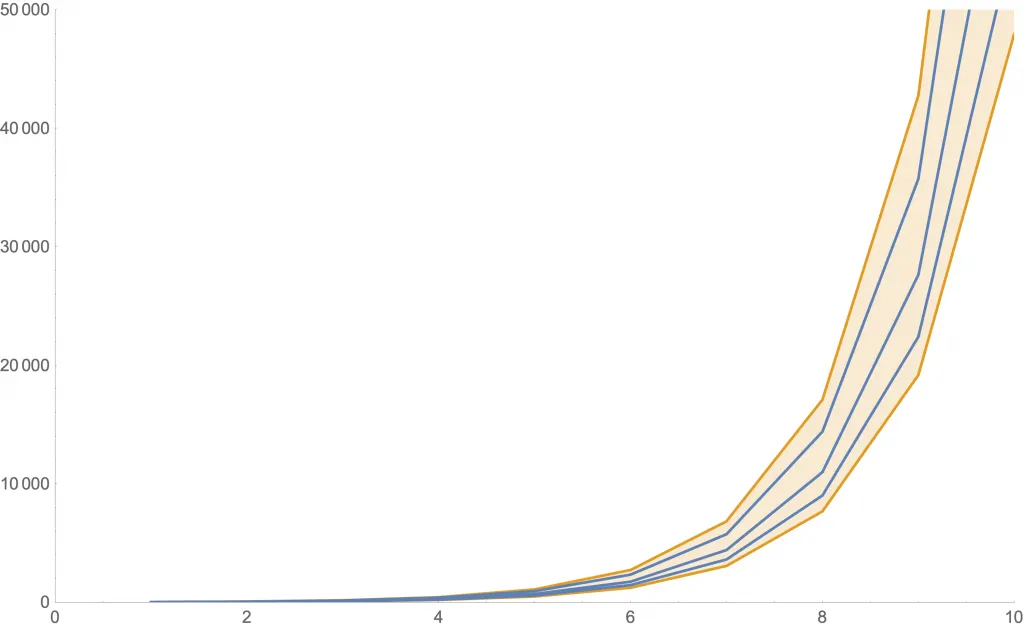
Las siguientes figuras muestran algunas simulaciones usando una distribución más realista (llamada «de Poisson») con distintos valores de . En cada una, se ven tres posibles curvas de nuevos contagios (azul) y la zona de 80% probabilidad (anaranjado).
Simulación con .
Simulación con .
Simulación con .
Para mejorar el modelo, podemos modificar el proceso de Bienaymé–Galton–Watson para que las probabilidades de contagio (y el ) cambien con el tiempo. Esto funciona de la siguiente forma: suponemos que inicialmente —en la generación 0— hay una cantidad fija de infectados. Cada uno de ellos transmite la enfermedad de manera independiente e idénticamente distribuida, como ya lo explicamos. Las personas que fueron infectadas por alguna de la generación 0 —estos nuevos infectados se conocen como generación 1— también van a contagiar el agente de manera independiente e idénticamente distribuida, pero esta manera puede ser distinta a la de la generación 0. Esto continúa indefinidamente: cada generación infecta a la siguiente de manera independiente e idénticamente distribuida, pero esta manera puede variar entre generaciones distintas. Esto es lo que se conoce como un proceso de Bienaymé–Galton–Watson dependiente de la edad. El cambio en el tiempo de estas distribuciones puede interpretarse como una consecuencia de las medidas de mitigación (como el distanciamiento social, las cuarentenas u otras), por lo que ahora hablaremos del en vez de .
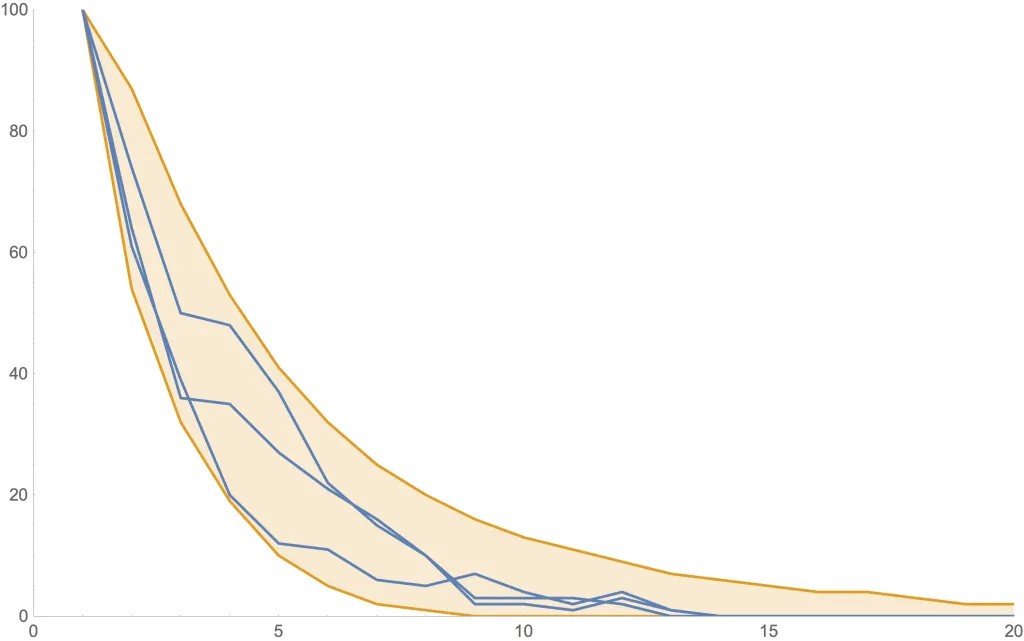
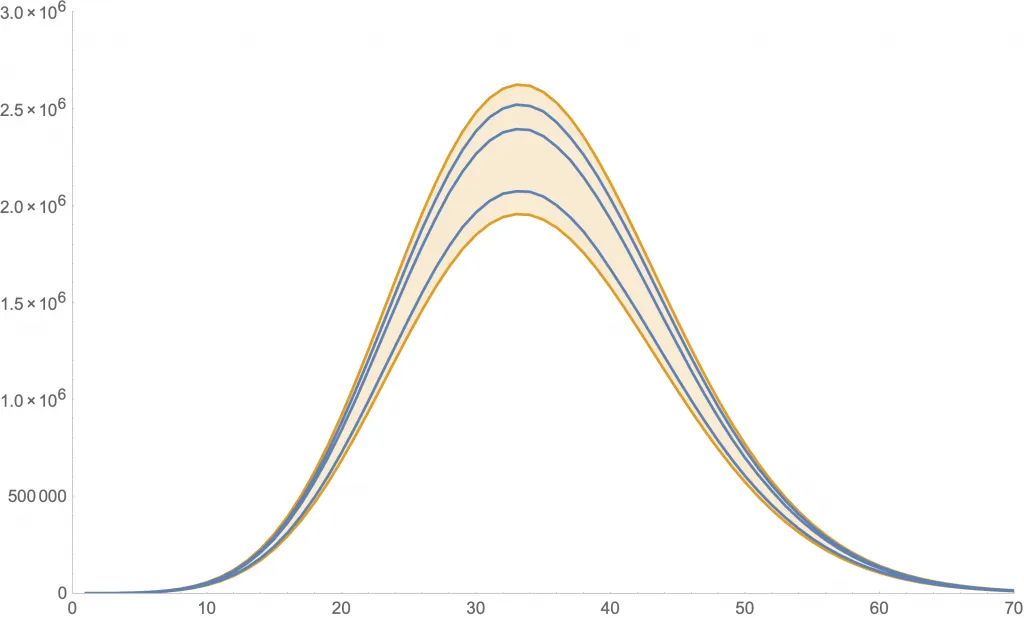
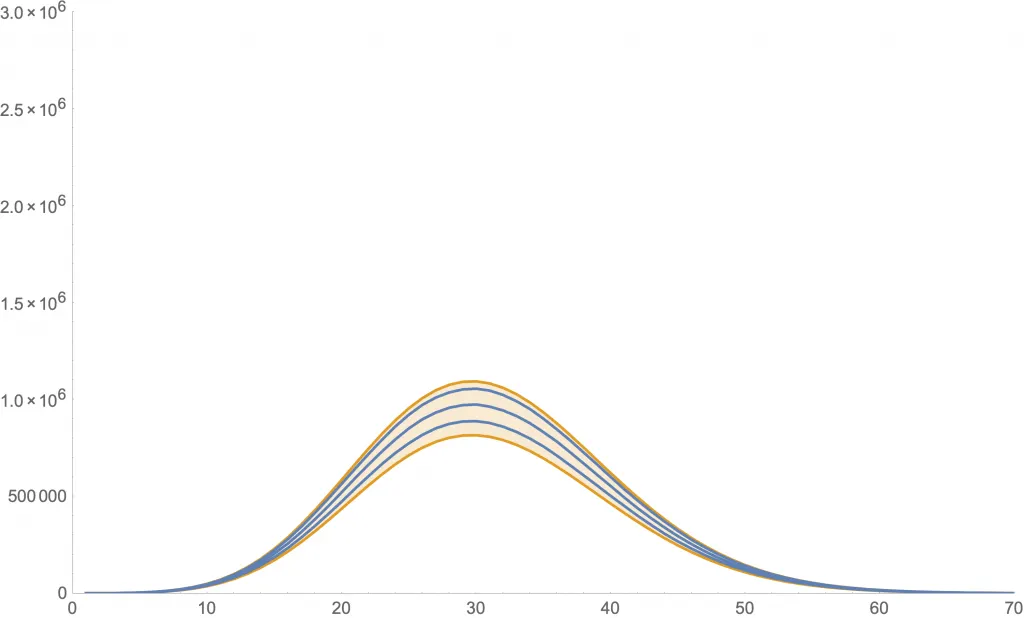
Las siguientes figuras muestran algunas simulaciones estos procesos que dependen de la edad. En cada una, se ven tres posibles curvas de nuevos contagios (azul) y la zona de 80% probabilidad (anaranjado). Además, en ambos casos la generación cero comienza con , pero se diferencian en la velocidad con la que decrece este parámetro.
Simulación con disminuyendo lentamente desde .
Simulación con disminuyendo rápidamente desde .
Estos modelos permiten ver claramente el rol del y por qué ocurre un cambio cuando el valor está debajo de 1. Pero incluso con las modificaciones que mencionamos, el modelo sigue siendo poco realista. En la siguiente sección complejizamos el modelo un poco, llegando a algo más cercano a lo que se usa en la realidad.
El momento de las ecuaciones diferenciales
Un modelo más sofisticado para modelar las curvas epidemiológicas se basa en ecuaciones diferenciales (tranquilidad: vamos a explicar qué significa esto cuando llegue el momento).
En esta sección presentaremos una versión muy simplificada, pero nótese que algunas variaciones de este modelo están siendo usadas, por ejemplo, en Chile para modelar el avance del COVID-19 por el país [4]. Este tipo de modelos se originan con el trabajo de Kermack y McKendrick en las décadas de 1920 y 1930. Lo que viene es una instancia sencilla de esta clase de modelos, pero notamos que hay muchas variaciones posibles (ver [2], [5] y [6], por ejemplo).
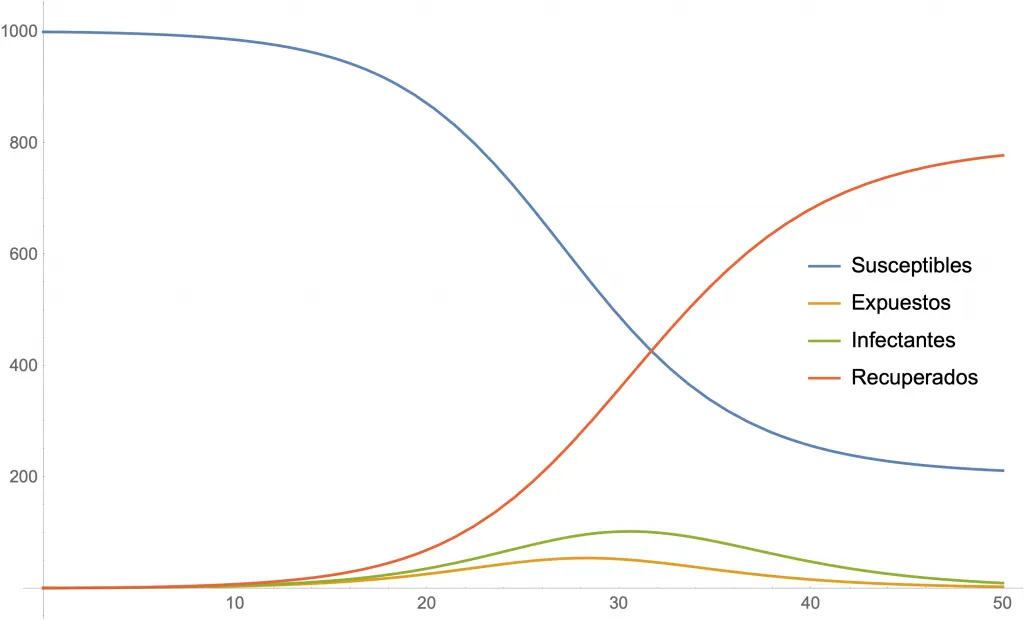
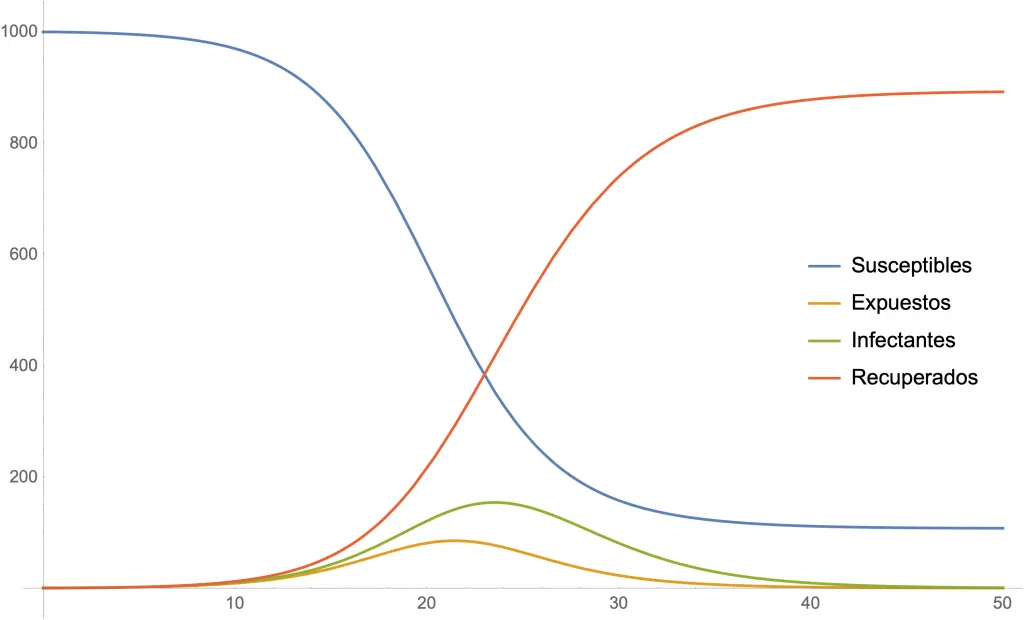
En el modelo llamado SEIR supondremos que la gente se divide en cuatro grupos: susceptibles , expuestos , infectantes y recuperados . Inicialmente, todas las personas parten como «susceptibles»» (no enfermos, pero con la posibilidad de contraer la enfermedad) y al adquirir el agente patógeno se convierten en «expuestos» (ya tienen el virus, pero por una ventana de tiempo todavía no son capaces de transmitirlo al resto). Los expuestos se convierten en «infectantes» (tienen el virus y contagian al resto) para luego ser «recuperados» (ya no contagian al resto, ya sea por haberse tratado, por haber adquirido inmunidad o... por haber muerto, aunque hay muchos agentes patógenos que pueden transmitirse incluso desde cadáveres).
Lo que interesa estudiar en el tiempo es, entonces, la proporción de todos estos grupos entre el total y cómo estas proporciones van evolucionando en el tiempo. La idea básica es la siguiente: queremos estudiar cuánta gente pasa de un estado a otro, digamos, cuánta gente pasa de ser «susceptibles» a ser «expuestos» de un día para otro. Sabemos que mientras más gente en el grupo «infectantes» haya, más fácil es que la gente pase a formar parte del grupo «expuestos» y se proyecta que el cambio sea más rápido. Al mismo tiempo, mientras menos gente susceptible haya, los infectantes son capaces de contagiar a menos gente.
Más precisamente, supondremos que todas las personas susceptibles visitan a todas las infectadas y que la probabilidad de que se transmita la enfermedad en cada encuentro es . Además, la proporción de expuestos que se infectan es y la proporción de infectantes que se recuperan es . Más allá de las cantidad exactas, el punto clave es que la forma de estimar «los cambios» en las cantidades de cada grupo para el día de mañana, depende del valor que estas mismas cantidades toman en el día de hoy.
Resumen del modelo SEIR.
Una forma matemática de expresar estas relaciones es mediante lo que se llama sistemas de ecuaciones diferenciales. Leer estas palabras juntas puede traer pesadillas a exestudiantes que pasaron por esto y no es necesario profundizar en muchos detalles. Pero, tratando de usar términos muy simples, tenemos un conjunto de cantidades que varían en el tiempo (la proporción de susceptibles, expuestos, etc.) y podemos escribir los cambios temporales de estas cantidades en términos de ellas mismas. La forma de escribir el «cambio temporal» de una función es lo que se llama la derivada de esta función. Escrito en fórmulas esto queda más o menos así:
Estos sistemas de ecuaciones pueden ser resueltos si son suficientemente simples. Si son muy complicados (como usualmente son estos casos), sus soluciones se pueden simular. En ambos casos, obtenemos las curvas que nos interesan y así tenemos dibujos que nos muestran la evolución del contagio en la población a través del tiempo. Además, el valor de se puede calcular directamente de los parámetros como , donde es la cantidad total de personas en la población estudiada (es decir, la suma de los susceptibles, expuestos, infectantes y recuperados).
Esta clase de modelos son mucho más ricos y presentan comportamientos mucho más variados que un simple «crecimiento exponencial». Como ya mencionamos, algunas versiones sofisticadas de estos modelos son usadas por los expertos para simular el comportamiento de la pandemia a futuro.
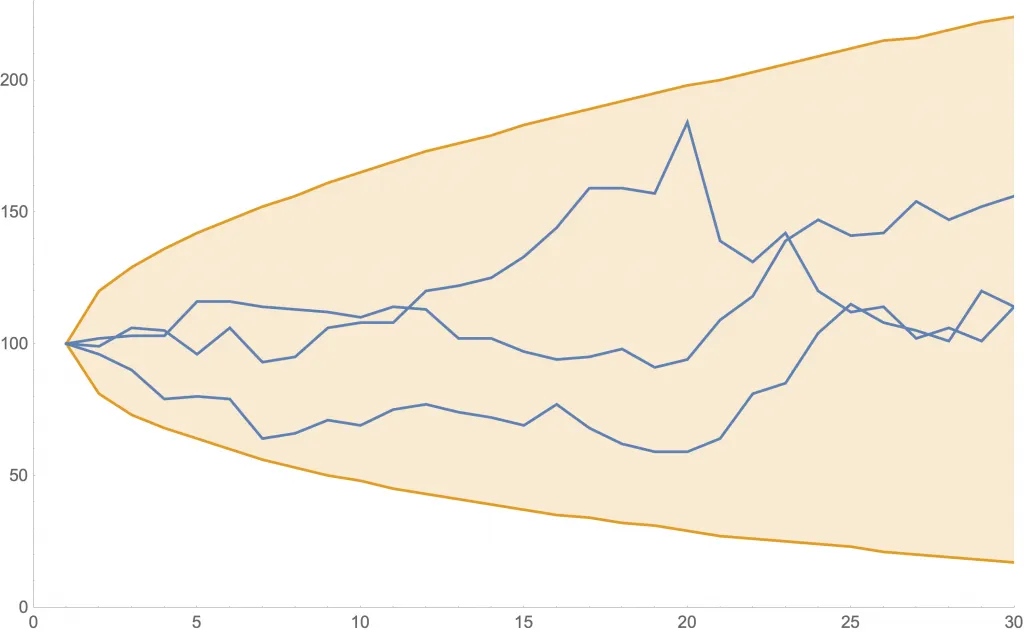
Las siguientes dos figuras muestran simulaciones para algunos valores de los parámetros. En ambas se usa , y cantidades iniciales de 999 susceptibles, 1 expuesto, 0 infectantes y 0 recuperados.
Simulación para (y ).
Simulación para (y ).
El problema de los modelos, sin embargo, es obvio: son simplificaciones de la realidad. Al ser simplificaciones, pueden proyectar panoramas muy alejados de lo que ocurrirá realmente. Esta limitación es conocida por toda persona que trabaje seriamente en modelación y es por ello que desde las ciencias se han desarrollado técnicas para hacer los modelos más avanzados. ¿Cuáles son estas técnicas?
La última chupá del mate
En todos los modelos anteriores, la idea subyacente era mantener el modelo muy simple. Los «procesos de ramificación» presentados en la primera parte son en esencia fáciles de estudiar, el sistema de ecuaciones presentado en la segunda parte es simple (¡tiene solo cuatro ecuaciones!). Para las simulaciones que se usan en la realidad, los modelos no tienen por qué ser tan resumidos y se pueden incluir muchos factores adicionales que permiten entender de mejor manera el avance de la enfermedad.
Comencemos con la inclusión de datos espaciales. En el modelo de ecuaciones presentado anteriormente, estábamos suponiendo que toda la población (gente que vive en Chile, digamos) se clasificaba en susceptible, infectante, etc. y que todos estos grupos interactuaban entre ellos al mismo tiempo. Este supuesto es poco realista: hemos visto cómo en Chile los brotes iniciales se han concentrado principalmente en algunas comunas donde hay muchos contagiados, mientras que en otras comunas hay pocos casos o ninguno. Esto no es tan extraño: la población está aglomerada en ciudades separadas unas de otras. Dentro de una misma ciudad es posible que un brote se extienda más fácil pero que en otras ciudades el brote no comience al mismo tiempo. Sin embargo, esto no es percibido por el modelo que describimos anteriormente.
Una forma de arreglar esto es agregar «compartimentos» que dividan a la gente. Por decir algo, en lugar de solo tener susceptibles, expuestos, infectantes y recuperados, podríamos tener «susceptibles de Santiago», «expuestos de Santiago», «infectados de Santiago» y «recuperados de Santiago» y hacer divisiones similares para cada ciudad o región del país. Si además tenemos datos de cómo interactúan estos grupos regionales, podemos simular cómo la infección va evolucionando dentro de cada región y, además, cómo la infección puede pasar desde una región a otra.
En la práctica, tenemos datos separados de población incluso a nivel de comuna y podemos estimar, por ejemplo (usando datos del transporte público), cuánta gente se desplaza entre una comuna y otra cada día para trabajar. Eso nos permite obtener simulaciones mucho más finas [4].
Estos modelos se pueden refinar incluso más. En modelos creados en el Reino Unido [3], aparte de la división territorial, tenemos división de las personas (usando datos precisos del censo) de acuerdo al lugar en el que viven, cuánta gente vive en cada hogar, su ocupación (estudiantes, trabajadores, etc.) y además su edad (jóvenes, adultos, ancianos). Entonces las interacciones que se pueden expresar son mucho más refinadas: los estudiantes podrían contagiarse en la universidad, luego contagiar a alguien de su familia, etc. Esta clase de divisiones además permite estudiar de forma certera el efecto de medidas que se pueden tomar para mitigar la expansión de una enfermedad. Por dar un ejemplo, si hay cuarentena y se suspenden las clases y se cierran los bares y restoranes, entonces los contagios entre estudiantes disminuirán, pero podrían aumentar los contagios entre personas de una misma familia dado que ahora pasarán más tiempo en el mismo lugar.
Hay que notar que este modelo no funciona simplemente en base a las ecuaciones que expresamos anteriormente, que solo consideran cantidades de personas. En cambio, esta clase de modelos realiza una simulación aleatoria de grupos anónimos de personas donde podemos estudiar el estado de cada «individuo» de manera separada, que después se agregan para obtener los datos globales que nos interesan. Por eso a esta clase de modelos se les llama modelos de «microsimulación».
Con este nivel de detalle, se puede estudiar de forma mucho más precisa el efecto de cada conjunto de medidas que se tomen en el avance de la enfermedad, algo absolutamente imprescindible para que las políticas públicas estén a la altura de la situación. Afortunadamente, simulaciones sofisticadas de este estilo ya se están realizando en el caso chileno [8], entregando información valiosa.
Más aun: como la modelación es un trabajo complejo, que necesita datos fiables y actualizados, que requiere mucha capacidad técnica y revisión por pares, no se puede esperar que sea una sola autoridad o un pequeño grupo de personas expertas quienes cumplan con todas las tareas (recolectar datos, procesarlos, construir el modelo, corregirlo...). Por ello, la colaboración entre la comunidad científica y las autoridades sanitarias es fundamental. Tal como lo destaca la Unesco, «la colaboración es crítica para compartir el conocimientos y los datos, así como para avanzar en la investigación sobre el COVID-19. En tiempos en que las barreras de comercio y transporte impiden el traslado de material crítico, es importante subrayar que se le debe dar el paso a la ciencia para que lidere la respuesta global a esta pandemia».
REFERENCIAS
1.
Jacob C. "Branching processes: their role in epidemiology" [Internet]. International journal of environmental research and public health. Molecular Diversity Preservation International (MDPI); 2010. Disponible en: https://www.ncbi.nlm.nih.gov/
2.
Scott E. Page y estudiantes. "Modelling COVID-19. Achieving Collective Intelligence Through Ensembles" [Internet]. Disponible en: https://sites.google.com/
3.
Neil M. Ferguson et al. "Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand." [Internet]. Disponible en: https://www.imperial.ac.uk/
4.
Tomás Pérez-Acle. Cuenta de Twitter personal [Internet]. Disponible en: https://twitter.com/
5.
Bruno Gonçalves. "Epidemic Modeling 101: Or why your CoVID-19 exponential fits are wrong" [Internet]. Disponible en: https://medium.com/
6.
Artículo "Kermack–McKendrick theory" de Wikipedia [Internet]. Disponible en: https://en.wikipedia.org/
7.
Martin Enserink y Kai Kupferschmidt. "Mathematics of life and death: How disease models shape national shutdowns and other pandemic policies" [Internet]. Revista Science; 2020. https://www.sciencemag.org/
8.
Marcelo Olivares et al. "Modelo de microsimulación de COVID-19 para evaluar estrategias de contención en nuevo webinar de Educación Ejecutiva" [Internet]. DII Universidad de Chile; 2020. Disponible en: http://www.dii.uchile.cl/
9.
Organización Mundial de la Salud. "Report of the WHO-China Joint Mission on Coronavirus Disease 2019 (COVID-19)" [Internet]. Disponible en: https://www.who.int/
10.
Mauricio Canals L., Andrea Canals C. y Cristóbal Cuadrado. "Informe COVID-19: Chile al 10.05.2020". Escuela de Salud Pública Universidad de Chile; 2020.