«El Nobel de Física 2016 fue entregado por la Real Academia Sueca de Ciencias a David J. Thouless, J. Michael Kosterlitz, y F. Duncan M. Haldane por sus descubrimientos teóricos sobre las estados topológicos de la materia y sus transiciones de fase».
Vivimos en un mundo tridimensional. Vivimos con alturas, anchuras y profundidades. Vivimos llenando cubetas con volúmenes. Nuestro espacio lo describimos por 3 coordenadas y, dentro de este espacio tridimensional, se definen las propiedades físicas de la materia. Pero, ¿qué pasaría si viviéramos en un mundo bidimensional?, ¿cómo cambiarían las propiedades físicas de los materiales que usamos día a día? Pregúntense, ¿cómo se ordenarían un conjunto de moléculas de agua si estuvieran obligadas a vivir en un plano? ¿Llamarían agua líquida a lo que queda sobre el plano?
Imaginarse la vida en dos dimensiones no es una idea nueva. Ya en el siglo XIX, mucho antes de la Casita del Horror VI [1], Edwin Abbott comentaba satíricamente la vida de un cuadrado (el Sr. A. Square) en un mundo plano bidimensional [2], donde el desarrollo de las actividades cotidianas distaba mucho del que tenemos en nuestro mundo tridimensional. En dos dimensiones, ¿cuál es el sentido de la palabra «horizonte»?, ¿se pueden superponer objetos?, ¿cuál es el símil bidimensional a un objeto tridimensional?, ¿podemos tener un estómago y digerir la comida? (la respuesta es no, #SpoilerAlert).
Dimensión desconocida
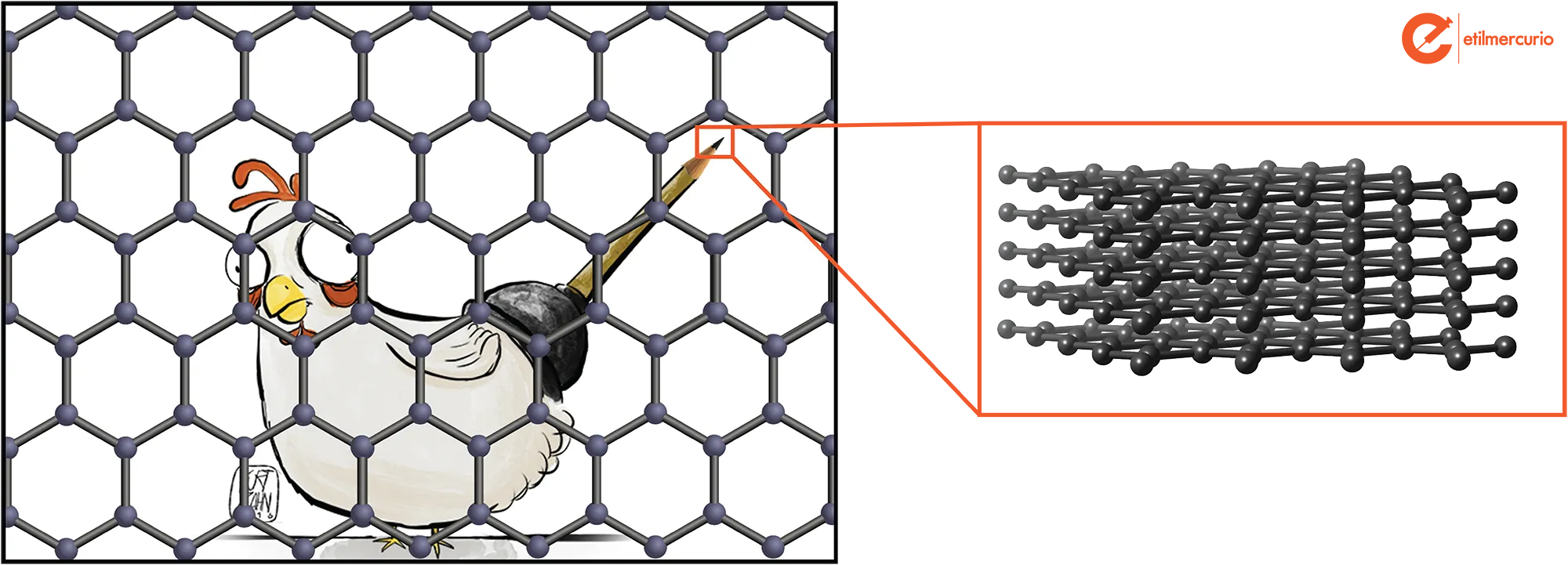
Izquierda: Grafeno; Derecha: Grafito
A pesar de que es un buen ejercicio jugar con la fantasía y la imaginación, preguntarse sobre esto es fundamental a la hora de comparar los comportamientos y propiedades físicas de los materiales en diferentes dimensiones. Un ejemplo de esto es el grafeno, una red de átomos de carbono bidimensional ordenados como alambre de gallinero [3]. En este material el transporte de partículas que portan carga (electrones) se debe realizar en un plano, y todas las posibles trayectorias de estas partículas escapándose fuera del plano no son permitidas. ¡Todo debe ocurrir en un plano! Así, la conducción de electrones en una muestra bidimensional es completamente diferente al transporte en una muestra tridimensional, incluso aunque ésta sea muy delgada. ¿Qué pasaría si uno pusiera varias capas de grafeno, unas sobre otras, construyendo un material tridimensional? Bueno, estarían construyendo la parte interior del clásico lápiz a mina, lo que llamamos grafito. A pesar de estar compuestos por el mismo material (carbono), el grafeno es duro y muy buen conductor de electricidad y de temperatura. Al contrario, el grafito se rompe (la punta de su Faber Castell Nº2 apenas comenzaban a responder la PSU les manda saludos) y conduce bastante mal la electricidad y la temperatura a través de sus capas de grafeno.
Entonces, al reducir una dimensión (pasar de un volumen a un plano, o de un plano a una línea), las propiedades físicas de la materia pueden ser diferentes. Otra manera de hacer que estas propiedades cambien, conocida por todos a la hora de tomar libaciones hidratantes con exceso de grupos OH (en mi caso, piscola... te amo), es calentar o enfriar la materia. El agua sólida pasa a ser líquida si se aumenta la temperatura a la que ésta se mantiene a presión ambiente, para llegar a ser vapor. A los estados sólido, líquido y gas se les llama fases de la materia, y al paso de una fase a otra, transición (un pequeño viaje en el tiempo a sus clases de química).
Hasta los inicios del siglo XX, todo andaba bien en esto de las transiciones de fase. Su comprensión, basado en las ideas profundas de Clausius, Boltzmann y Gibbs sobre la termodinámica y la mecánica estadística [4], había logrado explicar y predecir de manera clara y a la vez sencilla, cómo y cuándo una de estas fases pasaba a ser otra. Este cambio se lograba al variar un parámetro de control del sistema (como la temperatura a la cual se mantiene la materia o la presión a la cual está sometida ésta) por sobre algún valor específico. Lo sabemos bien cuando hervimos el agua (100º C a nivel del mar) o hacemos hielo (0º C a nivel del mar). Así, todas las fases conocidas parecían entenderse claramente.
Enter the quanta
De a poco comenzaron a aparecer evidencias de que no todo era paz y amor en el mundo clásico de las transiciones de fase. La materia parecía comportarse de manera particularmente rara en ciertos casos cuando se la sometía a condiciones extremas. Un ejemplo de esto es llevar a la materia a temperaturas extremadamente bajas. Allí algunos materiales conducían la electricidad sin ninguna resistencia a través de ellas, mejor que cualquier conductor en el mundo (incluso estos materiales pueden ser céramicos, parecidos a los que mi abuela protegía religiosamente cuando íbamos a verla a T A L C A). El helio en una de sus configuraciones estables parecía fluir sin tener ninguna resistencia al movimiento, como si no tuviera viscosidad. Partículas de ciertos gases podían acoplarse entre todas en una nube que parecía comportarse como una gran superpartícula [5]. Estos nuevos supermateriales presentaban desafíos de comprensión gigantes, y un nuevo entendimiento de la naturaleza, que llegó gracias a la descripción de ésta en términos de cambios discretos (quantas) en estos sistemas. Esto es lo que actualmente llamamos mecánica cuántica.
¿Donde entran los ganadores del Nobel de Física este año 2016? A principios de los 70, David J. Thouless, profesor en la Universidad de Birmingham conoció a John Michael Kosterlitz, que comenzaba una estadía postdoctoral. Juntos comenzaron a trabajar en cómo describir estadísticamente sistemas físicos en dos dimensiones espaciales. La manera en que comenzaron a estudiar el problema da para un libro. Mientras Thouless era empujado por pura curiosidad científica, Kosterlitz avanzaba movido por pura ignorancia de las complejidades en las que se estaba metiendo (como el mismo lo relata [6]). Al cabo de poco tiempo llegaron a entender que en estos sistemas de baja dimensión espacial había algo especial que permitía que éstos pudieran desarrollar fases diferentes a las usuales. Ese ingrediente extra tiene que ver con su topología.
Hoyos y Donas
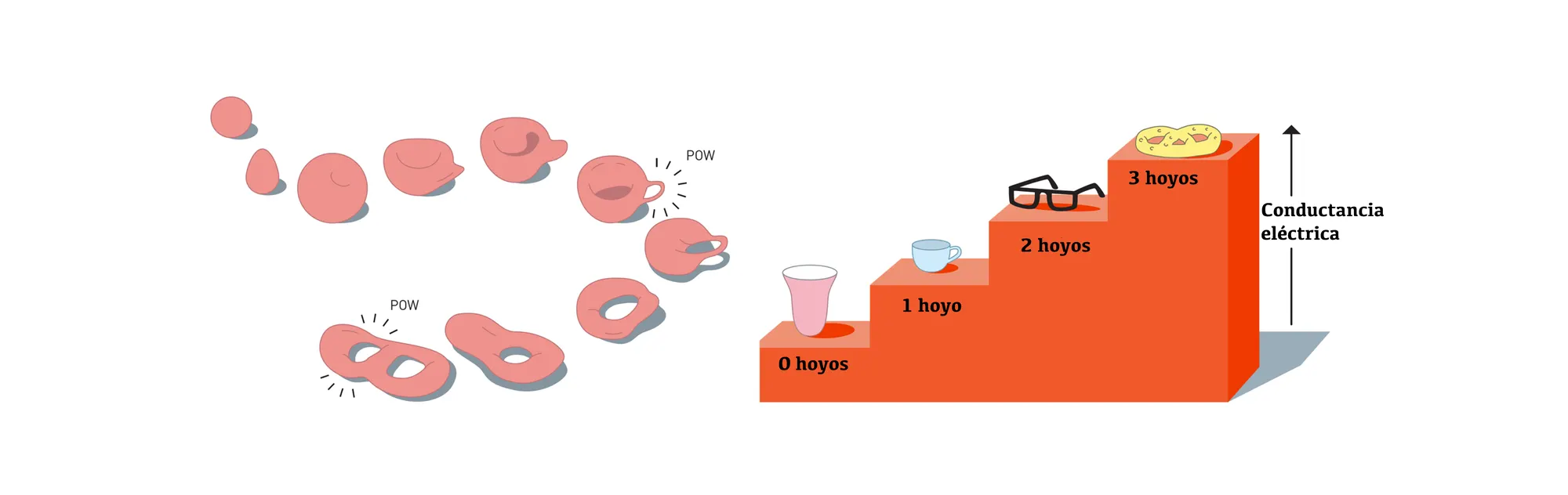
La topología es la rama de las matemáticas que se encarga de estudiar las propiedades de los objetos que no cambian cuando se deforman, estiran o contraen continuamente [7]. Estas propiedades se llaman invariantes topológicos. Los que han jugado con plasticina saben que es fácil deformar una bola de plasticina para transformarla suavemente, poco a poco, en un cubo o en un cilindro. Pero si quiero hacer una dona debo hacer un agujero, lo que constituye un cambio abrupto que no es continuo ni suave. Así una bola es topológicamente igual a un cubo, pero no a una dona. Solo porque una dona tiene un hoyo. O lo que llamamos de manera más elegante, un defecto.
Topológicamente, una dona es lo mismo que una taza de café. Fuente: Wikipedia.
Los cambios continuos no permiten cambios en la estructura «global». Aunque el objeto se deforme siempre se verá «igual»: una región con dos hoyos.
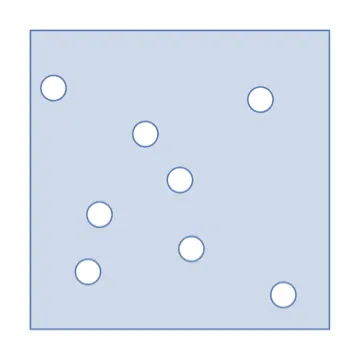
Thouless y Kosterlitz se dieron cuenta de aquello: los defectos que se generan en los sistemas bidimensionales no pueden desaparecer de manera suave, porque determinan la topología del sistema, y a la vez tanto determinan sus propiedades físicas [8]. Thouless y Kosterlitz mostraron que para temperaturas bajas estos defectos se ordenan de a pares, tal como se juntarían dos imanes de diferente polaridad, pero que a medida que la temperatura aumenta, se separan y viven solos moviéndose aleatoriamente por el material. Este es un cambio de fase de un estado ordenado a otro desordenado en dos dimensiones mediado por estos defectos topológicos, por lo que se llama una transición de fase topológica.
A temperaturas altas, los defectos no tienen un orden claro. Al bajar la temperatura, se ordenan de a pares.
Esto no se quedó ahí. La idea fue extrapolada por Thouless al estudio de la conducción de la electricidad en capas magnéticas delgadas a baja temperatura en presencia de campos magnéticos muy grandes [9], y por F. Duncan M. Haldane a una cadena de imanes atómicos [10]. En este caso, Thouless y Haldane, separadamente, mostraron que para que los electrones pudieran moverse por dentro de las muestras, la única manera de hacerlo era que la conductancia del material (es decir, la cantidad de corriente que puede pasar por el material por unidad de voltaje impuesto en los extremos de éste) estuviera discretizada. Esta discretización viene dada directamente por la necesidad de mantener constante un invariante topológico, que cambia discretamente (tal como el número de agujeros en la plasticina... de uno en uno). Así, estos invariantes topológicos, que no cambian si uno deforma o estira el material, determinan las propiedades físicas del mismo. Basado en los trabajos de Haldane [11], la comunidad científica propuso la posibilidad de usar la topología de un estado para «protegerlo» de perturbaciones: si fuerzo un sistema o realizo cambios sobre este que pueden ser grandes pero que no cambian los invariantes del sistema, entonces el estado de éste no puede cambiar. Así, podemos lograr que un sistema físico protegido topológicamente pueda conducir corriente incluso si este es calentado, deformado o alterado fuertemente. ¡La topología del sistema lo protege de los cambios!
Las ideas sencillas pero revolucionarias de Thouless, Kosterlitz y Haldane permearon la física, y abrieron una caja llena de preguntas y aplicaciones en óptica, magnetismo, y mecánica cuántica, y se expandieron a la cosmología, a la teoría cuántica de campos y la teoría de cuerdas. Y si usted cree que esto es algo que es exótico, piénselo bien. En especial cuando mire con desdén ese defecto topológico que se forma en la nuca de sus cabezas, que no puede hacer desaparecer nunca por vivir en dos dimensiones. «Remolino» le dicen.
Referencias
[1] Treehouse of Horror VI, http://www.imdb.com/title/tt0177842/
[2] “Flatland, a Romance in many dimensions”
[3] UYUI
[4] L.D. Landau, E.M. Lifshitz (1980). Statistical Physics. Vol. 5 (3rd ed.). Butterworth-Heinemann. ISBN 978-0-7506-3372-7.
[5] E.M. Lifshitz, L.P. Pitaevskii (1980). Statistical Physics, Part 2: Theory of the Condensed State. Vol. 9 (1st ed.). Butterworth-Heinemann. ISBN 978-0-7506-2636-1.
[6] J. Michael Kosterlitz ”Kosterlitz–Thouless physics: a review of key issues”, 2016 Rep. Prog. Phys. 79 026001
[7] Ryszard Engelking, General Topology, Heldermann Verlag, Sigma Series in Pure Mathematics, December 1989, ISBN 3-88538-006-4.
[8] J M Kosterlitz and D J Thouless. Long range order and metastability in two dimensional solids and superfluids.(Application of dislocation theory). Journal of Physics C: Solid State Physics, 5(11):L124, 1972.
[9] Qian Niu, D J Thouless, and Yong-Shi Wu. Quantized hall conductance as a topological invariant. Physical Review B, 31(6):3372, 1985.
[10] F.D.M. Haldane. Continuum dynamics of the 1-D Heisenberg antiferromagnet: Identification with the O(3) nonlinear sigma model. Physics Letters A, 93(9):464–468, 1983
[11] F.D.M. Haldane. Nonlinear Field Theory of Large-Spin Heisenberg Antiferromagnets: Semiclassically Quantized Solitons of the One-Dimensional Easy-Axis Néel State. Physical Review Letters, 50(15):1153, 1983.