Recordemos que Michael Bay destruyó a los Transformers. Lloremos un poco.
Bueno, ahora dejemos de sufrir y concentrémonos en algo que vale la pena recordar: el 21 de marzo se celebró el natalicio de Joseph Fourier. Lo recordamos recién ahora porque somos iconoclastas y nos rebelamos frente a la absurda tradición de recordar a la gente por algo tan arbitrario como su fecha de nacimiento (no es que se nos haya ido en collera y se nos haya pasado la fecha).
Fourier fue un matemático y físico francés al que le debemos más de lo que usted alguna vez imaginó deberle a cualquier francés. Incluso más que a los panaderos franceses que inventaron el pan francés (también conocido como pan batido o marraqueta, de acuerdo a fascinantes variaciones regionales).
Joseph «uno que otro segundo nombre francés» Fourier fue un alumno adelantado de cracks franceses como Joseph «otro segundo nombre pomposo» Lagrange y Pierre-Simon Laplace en la prestigiosa École Normale Supérieure de Paris.
Pero, antes de eso, quedó huérfano a los 9 años, fue educado por los benedictinos y estuvo preso brevemente durante el Régimen del Terror (y eso que nuestro amigo trabajó en uno de los comités revolucionarios). También fue asesor científico de Napoleón Bonaparte durante su expedición a Egipto y hasta se dedicó a escribir papers científicos en El Cairo cuando la flota británica cortó las rutas de regreso a Francia.
Cuando finalmente regresó a Francia, Fourier quiso retomar su puesto académico en la École Polytechnique, pero Napoleón insistió en darle cargos políticos y lo nombró prefecto del Departamento de Isère en Grenoble.
Nos imaginamos cómo debe haber sido el diálogo de Fourier con Napoleón.
—Por fin de vuelta a Francia. Ya no soportaba mascar arena todo el día. ¡Y el calor! ¡Uf! Debería investigar sobre cómo se propaga el calor...
—¡Joseph! ¡Mi fiel Joseph! Por fin regresaste a la bella Francia.
—Hola, Napo. El calor de Egipto me estaba matando. No esperes que te voy a acompañar de nuevo en una de tus aventuras...
—Tranquilo, ya no saldrás de Francia. Quiero recompensarte por tus servicios y tu lealtad.
—Oh, por favor. No fue nada: hago todo por nuestra patria...
—Mira, hace poco falleció el prefecto del Departamento de Isère. Yo sé que tú tienes todas las cualidades para reemplazarlo.
—¡¿Qué?!
—La paga es buena, estarás muy entretenido.
—¡Pero yo quiero investigar en la École Polytechnique!
—¿Estás despreciando mi recompensa, Joseph?
—Ehm... No, claro que no.
Al menos, en Grenoble tuvo tiempo para investigar. Y de hecho presentó su artículo sobre la propagación del calor en los cuerpos sólidos en diciembre de 1807.
Más aun: monsieur Fourier descubrió que al representar una función matemática como una suma de funciones trigonométricas se simplificaba enormemente el estudio de la transferencia de calor. De aquí nace el análisis de Fourier, que tiene consecuencias desde prácticas hasta teóricas. Intentaremos develar un poquito de cada una de estas capas a continuación.
Fourier S01E01
El análisis de Fourier permite, entre otras cosas, representar cualquier función mediante una aproximación realizada a partir de sumas de otras funciones trigonométricas más simples. El análisis de Fourier es una de las herramientas más hermosamente formuladas de la historia del mundo mundial. Sin embargo, está escondida detrás de un mogollón de ecuaciones y términos que asustan hasta a los mechones y mechonas más valientes.
Ewwww. Pero en vez de enredarnos con tanta ecuación ininteligible, veamos cuál es la idea detrás de ellas.
Imagine que una mañana va a uno de esos lugares en que, en vez de una marraqueta con arrollado (la cantidad de dientes que tiene una marraqueta queda para otro post), sirven smoothies al desayuno (entender por qué usted haría eso nos resulta más difícil que entender las ecuaciones anteriores). Un smoothie, según nuestro alumno de intercambio en práctica, es la forma siútica, innecesaria y extranjerizante para referirse a un batido con helado.
Suponga ahora que, a regañadientes, probó el smoothie y resulta que lo encontró sabrosísimo. ¡Qué delicia! Cuando fue a pedir otro se dio cuenta del valor de ese vaso y le dolió hasta el píloro. Así que decidió comprar los ingredientes en la feria libre para prepararse ese manjar en la comodidad de su hogar (y a una fracción del precio). Sin embargo, cuando fue a pedirle la receta al amable joven que lo atendió, este se negó a entregar tan secreta información. La decepción se apoderó de usted al no poder saber qué frutas se combinaron en ese exquisito, cremoso, bello y desconocido smoothie.
¡Qué útil sería en ese momento tener una batidora inversa, que tomara el smoothie, una papilla o un puré y le dijera los ingredientes que lo componen!
Aquí es donde aparece la utilidad de la transformada de Fourier. La transformada de Fourier toma un patrón basado en el tiempo, mide cada ciclo posible y devuelve la «receta de ciclo» general. Volviendo al ejemplo anterior, es como si le pasáramos el smoothie y nos entregara una lista de sus ingredientes con sus cantidades precisas.
Lo que tienen en común los mp3 y las falsificaciones de Pollock
Sabemos lo que está pensando. «Ya, ¿pero cuándo voy a usar esa brujería en mi rutina diaria? Mientras no sirva para descifrar el misterio del amor y de la muerte, me parece una pérdida de tiempo». Lo sabíamos desde antes de empezar a escribir este post, por lo tanto nos preparamos.
Otro día más en que prefiere no descubrir algo nuevo.
La verdad es que la aplicación de la transformada de Fourier está muy presente en nuestra vida, sobre todo en el ámbito tecnológico.
Como explicamos anteriormente, la finalidad de la transformada es «simplificar» una función para entregar una aproximación. ¿Alguna vez ha escuchado una canción en formato FLAC? Dicen los entendidos en música que es la representación más exacta del sonido que fue grabado en el estudio. La gran desventaja de este formato es su tamaño. Recordemos que durante la década 1990 la velocidad de la red distaba mucho de las actuales: descargar un archivo de más de 10 MB implicaba largos y angustiosos minutos de espera, además de poner especial cuidado para mantener al resto de la familia lejos del teléfono.
Precisamente por la dificultad de difundir sonidos digitales de forma sencilla, ingenieros alemanes del Instituto Fraunhofer IIS trabajaron para obtener un archivo de sonido de menor tamaño, pero sin una gran pérdida de calidad. El truco que ocuparon es el siguiente: tomaron un archivo lossless y lo dividieron en pedazos de un tamaño determinado. Sobre cada uno de esos trozos aplicaron una versión de la transformada de Fourier, conocida como transformada de Fourier discreta, que devuelve los «ingredientes» del segmento y reemplaza el original.
La ventaja de la transformada es que indica qué notas contribuyen mayormente a crear la canción, por lo que podemos conocer cuáles son esenciales para reproducir correctamente el sonido original. Las notas altas no son tan importantes, ya que no podemos escucharlas (a menos que usted tenga un súper oído), por lo que se eliminan en el proceso. Esto permite una mayor compresión en la información y una reducción en el tamaño del archivo.
Y... Voilà ! Así nació el formato mp3 que, con su reducido tamaño, permitió que muchos pudiéramos descargar y compartir ilegalmente toda la música que nuestros roñosos discos duros de 10 GB nos permitían.
Las aplicaciones de reconocimiento de canciones (como la pionera Shazam) funcionan de forma similar. Dividen la música en segmentos y utilizan la transformada para obtener las notas «ingredientes». Luego buscan en una gigantesca base de datos para ver si esta «huella» de notas calza con alguna de las que se tiene almacenada. Lo mismo ocurre con el reconocimiento de voz utilizado por su smartphone favorito, donde se compara las notas en su hablamiento con un listado conocido de palabras.
Algo similar ocurre con los archivos de imágenes. Probablemente usted ha notado que existen distintos formatos de imágenes, cada uno con sus calidades y tamaños: el formato jpeg es el mp3 de las imágenes. Al tomar una imagen sin compresión y convertirla a jpeg, la imagen se divide en segmentos de 8 x 8 pixeles y se va reconstruyendo con los ingredientes esenciales, logrando una gran disminución en el tamaño del archivo con una leve reducción en su calidad.
Excepto en los memes que envía su tía favorita al grupo de la familia.
En general, las aplicaciones de esta herramienta en la ciencia abarcan desde la dinámica de fluidos hasta la astronomía, pasando por el análisis de estructuras celulares, de señales digitales y el estudio de la acústica de los instrumentos musicales. La aplicación de la transformada incluso permitió reconocer cuadros falsificados de Jackson Pollock descifrando los químicos presentes en la pintura (1).
Así que cuando escuche su disco favorito en su reproductor de mp3 o disfrute de unos memazos de gran calidad, recuerde que detrás de esto se encuentra esta poderosa herramienta.
De ecuaciones diferenciales y la velocidad del Transantiago
Por supuesto, el trabajo de Fourier no solo sirve para escuchar esas maravillosas obras de música trap. Su trabajo ha sido muy relevante en la matemática más teórica. De hecho, la idea fourieriana de «descomponer» funciones sigue siendo influyente en muchos contextos matemáticos. Entre estos, destaca la teoría de ecuaciones diferenciales: aquí, el análisis de Fourier juega un rol fundamental.
Primero, le explicaremos qué es la derivada de una función.
Imagine que usted, que usa frecuentemente el transporte público santiaguino, quiere estimar cuán rápido se mueve su línea de Transantiago preferida. Como usted no es uno de esos millennials que le confían su vida a sus smartphones y a sus apps, las únicas herramientas que posee son un lápiz, papel y un reloj. Por otro lado, sabe que cada cuadra del centro capitalino suele medir entre 100 y 150 metros, así que decide irse a la segura y estima una longitud de 125 metros por cuadra, o un kilómetro por cada 8 cuadras.
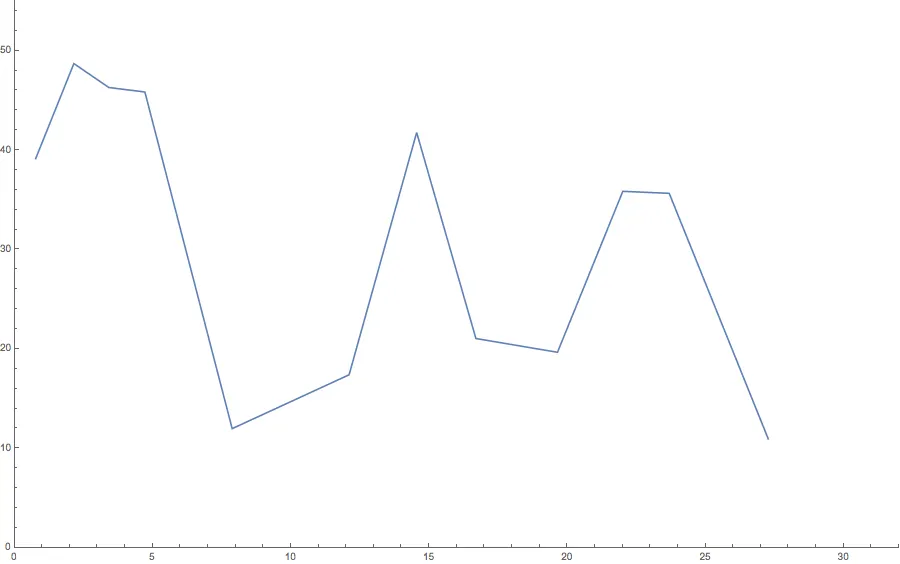
Recordando que la rapidez es la tasa de cambio de la distancia recorrida, decide registrar el tiempo que tarde en bus en recorrer cada kilómetro, es decir, cada tramo de 8 cuadras como primera estimación. Luego calcula el cociente entre la distancia recorrida (un kilómetro) y el tiempo que tardó el bus en recorrerla (que usted midió con el reloj). Graficando el resultado, obtiene algo como esto:
Rapidez medida cada ocho cuadras.
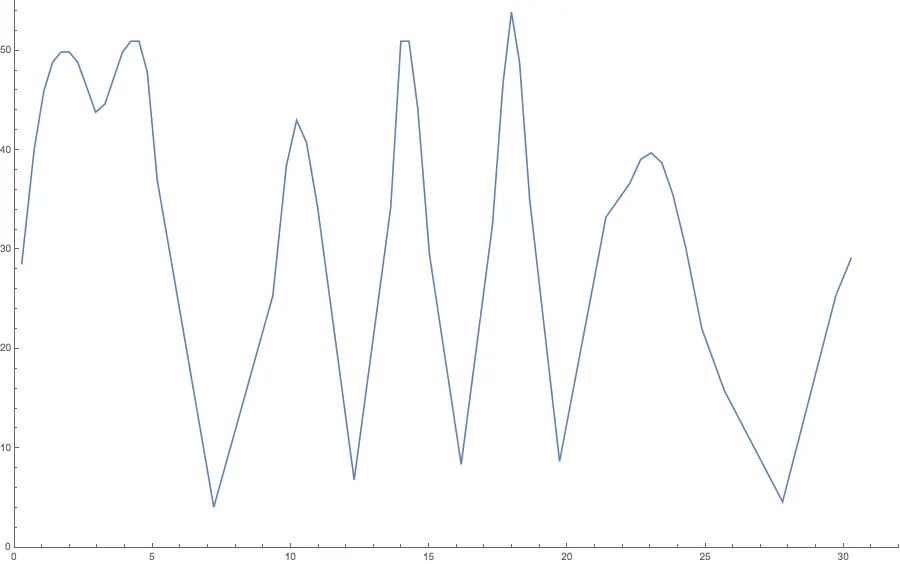
Como no está satisfecho con esa aproximación, decide repetir el ejercicio, pero esta vez por cada dos cuadras recorridas, obteniendo un gráfico así:
Rapidez medida cada dos cuadras.
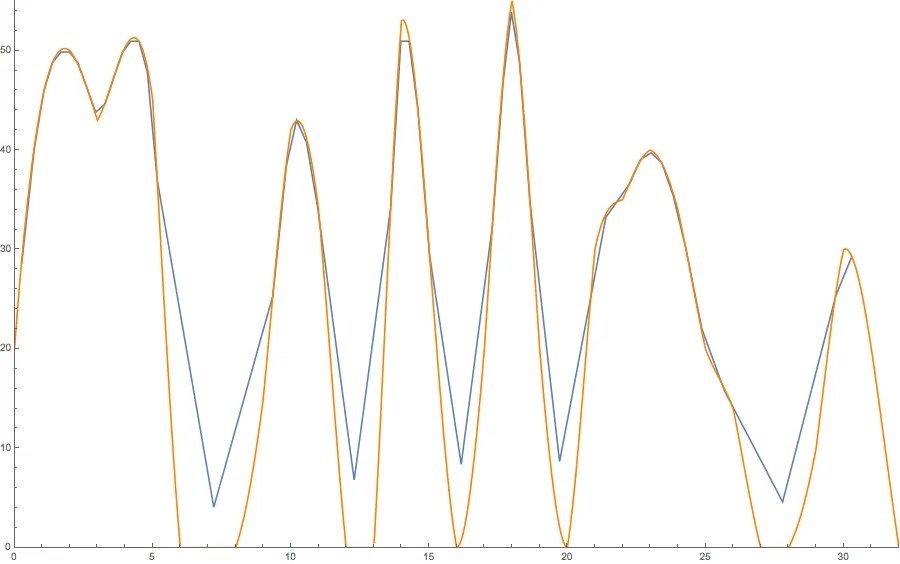
Podría continuar ahora por cada cuadra o media cuadra. Si tuviera una forma más precisa de medir la distancia recorrida (como por ejemplo el GPS de un smartphone), podría calcular la rapidez en intervalos de tiempo cada vez más pequeños. Esta última idea es precisamente la definición de la derivada de una función: su tasa de cambio, definida como la «rapidez» de la función en intervalos de tiempo arbitrariamente pequeños. La derivada de la posición es la velocidad y la derivada de esta última es la aceleración. En nuestro ejemplo, la verdadera rapidez, comparada con la que fue medida cada dos cuadras, se ve así:
Rapidez medida cada dos cuadras (azul) y verdadera rapidez medida en tiempos arbitrariamente pequeños (anaranjado).
Una ecuación diferencial es un tipo de ecuación funcional. Es decir, una ecuación en la que la incógnita es una función. Las ecuaciones diferenciales relacionan una función incógnita con sus derivadas. Un ejemplo de ecuación diferencial es la segunda ley de Newton que relaciona la aceleración con la fuerza. Para saber cómo se mueve el sistema —su posición en el tiempo— hay que recuperarla a partir de información sobre su aceleración que es la derivada de su derivada (o segunda derivada).
La derivada es una operación complicada sobre una función y, por lo tanto, las ecuaciones diferenciales son difíciles de entender. La transformada de Fourier es importante en esta teoría porque transforma la derivada de una función en una operación muchísimo más simple, es decir, en una multiplicación (spoiler por si sabe álgebra lineal: esta idea es muy profunda y tiene que ver con el teorema espectral para operadores no acotados, que es una amplia generalización de la idea de diagonalizar matrices simétricas).
De esta forma, al usar la transformada de Fourier en una ecuación diferencial podemos transformar una ecuación complicada en una ecuación más sencilla que muchas veces se puede resolver (o al menos entender) mediante métodos conocidos.
Fourier caluroso
El desarrollo de esta teoría por parte de Fourier tuvo el propósito de plantear (¡y resolver!) un problema que estaba aquejando a los científicos del siglo XVIII: cómo modelar el calor mediante ecuaciones. Gigantes como Lavoisier, Laplace y Biot dedicaron parte de sus estudios a este problema, específicamente al problema de entender cómo se comporta el calor en un sólido.
Una de las ideas primordiales refinadas durante esa época fue la siguiente: la tasa en la que un sólido pierde calor (o sea, su derivada) es proporcional a la diferencia de calor entre el sólido y el ambiente.
Esto fue formalizado por Fourier como una ecuación diferencial que relaciona la temperatura con la derivada de la temperatura, lo que se conoce como la ecuación diferencial del calor. Fourier desarrolló las técnicas del análisis de Fourier, de las que hablamos en la sección anterior, justamente para poder resolver ecuaciones de este tipo. Pero es notable que el planteamiento de ecuación del calor hecho por Fourier, por sí solo, ha sido enormemente influyente. Esta ecuación se ha usado en muchísimas aplicaciones en la realidad, no solo para modelar fenómenos de calor: ideas similares se usan para modelar fenómenos eléctricos, económicos, etc. y cualquier cosa que tenga «difusión».
Para terminar, hay que mencionar otro descubrimiento notable de Fourier. En 1824 calculó cuán caluroso debería ser un objeto del tamaño de la Tierra ubicado a la misma distancia que existe entre la Tierra y el Sol si solo consideramos la energía que recibe vía solar. Llegó al resultado contraintuitivo de que dicho objeto debería ser muchísimo más frío que lo que es la Tierra normalmente. Tratando de buscar una explicación a este fenómeno planteó que la atmósfera terrestre actuaba como un «aislante» y esto le permitía conservar de mejor forma el calor recibido por el Sol. Es decir, monsieur Fourier descubrió el efecto invernadero, tan ineludible a la hora de discutir del cambio climático.
Referencias
1.
2.
Narasimhan TN. Fourier’s heat conduction equation: History, influence, and connections. Rev Geophys. 1999;37(1):151–72. Disponible aquí.
3.
Fourier J (1824). "Remarques Générales Sur Les Températures Du Globe Terrestre Et Des Espaces Planétaires". Annales de Chimie et de Physique. 27: 136–67.