Nicanor Parra fue un visionario y un rupturista en muchos aspectos. Inventó un tipo de poesía —la antipoesía—, rompió los cánones de lo lírico y hasta fue capaz de morir mirando hacia el mar estando en Santiago. Lo que no logró hacer fue popularizar el concepto de desviación estándar.
Espera, espera. KHÉ. ¿Cómo pasamos de la antipoesía a la desviación estándar? ¿Quisaweá?
¿Recuerda usted esa frase popularizada por internet y atribuida a Nicanor Parra? Si tú lo deseas puedes volar «Hay dos panes. Usted se come dos. Yo ninguno. Consumo promedio: un pan por persona». Esta frase es matemáticamente cierta, pero también matemáticamente incompleta. ¿Por qué? Porque se usa un solo número —el «promedio» de consumo de panes— para resumir la situación de la totalidad de las personas. Como todo resumen, puede ser bastante fiel a la realidad o bien puede estar incompleto y esconder sutilezas. ¿Cómo saber entonces cuándo un promedio nos está dando información fiel o no?
Para tener un panorama completo, lo mejor sería presentar otros datos que resuman aspectos más profundos de la situación: esto nos permitiría tener una mirada más global y certera de lo que están informando.
¿Y de dónde sacamos estos números?
Entrando al bello (?) mundo de las medidas de tendencia central y las medidas de dispersión.
Promedio
Si usted fue al colegio (algo que no nos queda del todo claro para mucha gente), seguramente sabe lo que es un promedio. Si estuvo coqueteando con repetir —o de plano se echó un año— sabe que para calcular un promedio cada valor es importante y pesa lo mismo.
Un promedio, o formalmente llamada media (medius promedius), es una suma de elementos dividida por la cantidad de elementos sumados. El promedio, en general, va a ser un número que está por sobre algunos de los datos considerados y bajo otros. Siguiendo el mismo ejemplo del colegio, si usted sacó promedio 6,0 en Historia y Geografía (acaso viejazo), lo más probable es que usted haya tenido notas sobre 6,0 y notas bajo 6,0, y no necesariamente solo notas 6,0. O, tomando la cita referenciada al principio, no todos nos vamos a comer la misma cantidad exacta de panes, pues, señor Parra.
Como mencionamos al inicio, el promedio es una de las formas de resumir una cantidad (posiblemente enorme) de datos en un solo valor. A este tipo de «resúmenes» se les llama medidas de tendencia central y la idea es que el valor esté «al centro» de todos los datos. ¿Simple, no?
Pues no tanto. Como decíamos al principio, hay que tener cuidado con la información que de verdad nos entrega el promedio.
Pequeño manual de cómo NO interpretar promedios
Veamos, con unos ejemplos, cómo la interpretación de un promedio (algo simple en apariencia) puede llevar a situaciones muy exóticas.
El año 2014, La Tercera publicó un titular en su portada, sobre una medida de consumo de marihuana a nivel nacional. Mencionaba que ocho regiones presentaban un consumo «superior al promedio nacional». Dado que en 2014 el número de regiones chilenas era 15, el titular está diciendo que el consumo de, más o menos, la mitad de las regiones está por sobre el promedio nacional.
No hay que ser muy vivaracho para darse cuenta de que esto no es muy noticioso: solo está diciendo que aproximadamente la mitad de una serie de 15 datos (uno por región) supera el promedio. Volviendo al ejemplo de su promedio en Historia y Geografía, es como si dijera que ocho de las 15 notas que tuvo durante el año eran superiores a 6,0 y las otras siete eran iguales o inferior a 6,0. Pues, claro: así funcionan los promedios, duh.
Pero mira esa weá, hermano.
Otro ejemplo ocurre con frecuencia en la prensa chilena a la hora de analizar los resultados de la PSU. A fines de cada año, no es extraño ver un titular alarmista del tipo «la mitad de los estudiantes sacó menos de 500 puntos». La verdad es que el sistema de puntajes de la PSU está diseñado para que el promedio de los puntajes se sitúe siempre alrededor de 500 puntos y que la distribución de puntajes sea «simétrica» en torno a ese valor (en ñoño más precisamente, se aproximan los datos a una distribución normal con media 500). No es tan extraño, entonces, que la mitad de los puntajes esté bajo el promedio. O sea, de noticioso, no hay mucho.
De cada diez titulares de prensa que hablan de estadística, cinco son la mitad
Pero, aparte de estos casos, hay errores un poco más sutiles que pueden ocurrir a la hora de interpretar promedios. Usemos un ejemplo de juguete, llevando el caso del poema inicial al extremo. Supongamos que queremos medir el consumo de pan semanal por persona. Les preguntamos a 10 personas: nueve no consumen pan en lo absoluto y una sola persona consume 100 panes a la semana. El total de panes consumidos entre estas 10 personas es 100, por lo que el consumo semanal promedio es de 10 panes por persona. Fíjese que, a diferencia de los casos anteriores, acá es falso que la cantidad de personas bajo el promedio es cercana a la mitad. De hecho, casi todas las personas (el 90%) consumen una cantidad de pan que está bajo el promedio.
Si bien este ejemplo está cocinado porque estamos incluyendo a una sola persona que empuja todo el promedio hacia arriba, no es tan caprichoso plantearse casos así. En 2017, el Instituto Nacional de Estadísticas publicó que, dentro de la población ocupada, el sueldo promedio es de $\$554.493$. Sin embargo, al mismo tiempo, publicó que la mitad de las personas tenían un sueldo inferior a $\$379.673$. Muchísima diferencia.
¿Qué falla acá? ¿Por qué el promedio no está representando fielmente los datos? ¿Cómo se puede arreglar?
Medianas y desviaciones estándar
Si bien mencionamos que el promedio es una medida de tendencia central, resulta que no es la única medida de tendencia central. Existen otras formas de resumir un conjunto de datos que en algunos casos pueden entregar información más «certera» que el promedio.
Veamos un ejemplo: la mediana se define como el valor que está «en la mitad» de un conjunto de datos. Por ejemplo, en el caso de los sueldos en Chile, si bien el promedio es $\$554.493$, la mediana de los sueldos es $\$379.673$. Esto significa que la mitad de las personas que trabajan ganan a lo más $\$379.673$ y la otra mitad gana al menos $\$379.673$. En datos que varían demasiado, la mediana puede dar una aproximación más realista del panorama global.
En un país como Chile, donde la desigualdad económica y social es altísima (1), utilizar promedios puede interpretarse como una distorsión antojadiza de la realidad. Al respecto se ha escrito ampliamente (2), sobre todo cuando se consideran los promedios de datos de la encuesta Casen considerando la inmigración (3). Utilizar promedios para dar a conocer una realidad nacional no ayuda a comprender la situación, más bien genera confusión y puede distorsionar la toma de decisiones.
Pero esto no significa que el promedio sea inútil. El promedio, como manera de resumir un conjunto de datos, funciona bien cuando los datos están todos muy «concentrados» en torno a un valor central. Esto es cierto en el caso de estudiar el consumo de marihuana en 15 regiones, o en el caso de la PSU, donde los puntajes por diseño están distribuidos de manera muy regular. En el ejemplo de los panes o el de los sueldos en Chile, los datos no están bien distribuidos: existe un número pequeño de datos que son muchísimo más altos que casi todos los otros. Entonces, estos datos extremos empujan el promedio hacia arriba y hacen que el promedio, por sí solo, no represente fielmente la realidad.
Claramente este es un buen ejemplo de lo anterior, porque muchos acá aportamos con valores negativos :(
Por suerte, existe una forma de medir cuán bueno es un promedio (malditos estadísticos que pensaron en todo): son las llamadas medidas de dispersión y posiblemente la más popular es la desviación estándar.
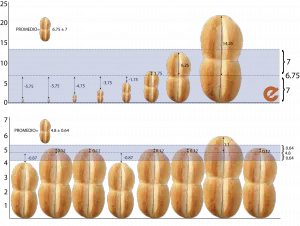
La idea detrás de las medidas de dispersión es bastante intuitiva y podríamos entenderla simplemente como «qué tanto se dispersan o separan mis valores respecto a una medida de tendencia central» (por ejemplo, la media). Con panes se vería algo así. La línea punteada del centro es el promedio, y toda el área azul es la desviación estándar, es decir, cuanto se dispersan los panes respecto al delicioso pan promedio. En el primer ejemplo, el pan más grande es una marraqueta como todas, pero poderosa. En el segundo ejemplo todos los panes son similares, por lo tanto, la desviación estándar es mucho más pequeña. Eso significa que efectivamente a todos nos llega algo.
Nota: estamos aún discutiendo la unidad de medida para la panitud.
La idea de fondo es que si la medida de dispersión es baja, los datos se parecen mucho al promedio (y, por lo tanto, se parecen mucho entre sí). Por el contrario, si la medida de dispersión es alta, los datos están alejados entre sí y es posible que el promedio no sea un resumen fiel de los datos. Esto es exactamente lo que pasa en los ejemplos de los panes y los sueldos: la desviación estándar es alta y, por lo tanto, los datos no se parecen al promedio.
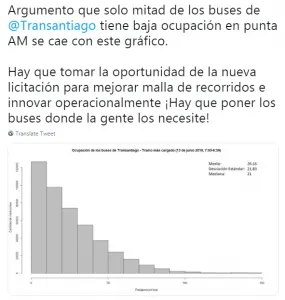
La información que nos entrega la desviación estándar es útil porque ayuda a pensar qué tan distintos son los casos que componen el promedio. Podemos poner en práctica lo aprendido con un ejemplo. Acá un académico intenta argumentar, con un gráfico, que existe una falla en el diseño de Transantiago pues la mayoría de los buses del Transantiago tienen muy baja ocupación en la hora punta de la mañana.
¿Profesor de Estadística I?
Sin embargo, en el gráfico se muestra el promedio, la mediana y la desviación estándar. El promedio en este caso es de 26,16 pasajeros por bus, la mediana es 21 pasajeros por bus y la desviación estándar es de 21,83 pasajeros por bus. Notamos entonces que la desviación estándar es altísima, incluso similar al promedio. Por lo tanto, los datos no tienen por qué acercarse al promedio en general. El gráfico por sí solo no permite sacar conclusión alguna pues los datos presentan una dispersión demasiado grande.
Este tipo de distribuciones, así como el ejemplo del sueldo el Chile o del capital per cápita, son particularmente asimétricas. Es decir, existe una distribución muy desigual en la población o bien hay unos pocos casos con valores extremos que distorsionan las medidas de tendencia central. En todos los escenarios, pero especialmente en estos, es fundamental que las medidas de dispersión estén explicitadas en los datos.
Moraleja
No hay una sola forma de resumir los datos en un solo número. El promedio es uno de los más populares para comunicar, pero muchas veces no interpreta en forma correcta un conjunto de datos. Utilizar un promedio de esta forma puede causar desde errores jocosos a graves distorsiones en la comprensión de la realidad. La mediana se define como «el valor que divide a los datos en dos mitades» y muchas veces es más útil mirar este valor en lugar del promedio.
¿Significa esto que el promedio es siempre inútil? No, por supuesto que no. El promedio es sencillo, fácil de entender y entrega mucha información. El promedio es nuestro amigo. Pero sería aconsejable siempre acompañar el promedio de la desviación estándar para evaluar si hay una gran dispersión de los datos (o sea, si la desviación estándar es alta). Es decir, un promedio explica bien una situación si es acompañado por una medida de desviación pequeña: exíjala a su periodista más cercano.
Referencias
1.
OCDE, 2018. Income Distribution Database. Disponible en http://www.oecd.org/social/income-distribution-database.htm
2.
García P, Pérez C (2017). Desigualdad, inflación, ciclos y crisis en Chile. Estudios de Economía vol.44 no.2 Santiago dic. 2017. Disponible en https://scielo.conicyt.cl/scielo.php?pid=S0718-52862017000200185&script=sci_arttext&tlng=en
3.
Cabieses B et al (2017). Brechas de desigualdad en salud en niños migrantes versus locales en Chile. Revista chilena de pediatría vol.88 no.6 Santiago dic. 2017. Disponible en https://scielo.conicyt.cl/scielo.php?pid=S0370-41062017000600707&script=sci_arttext