Queremos comenzar el post de hoy con un video. Sabemos que muchos de ustedes lo reconocerán de inmediato, mientras que el resto se deleitará por primera vez con un comercial que, quizás sin quererlo, acercó la física a la gente.
Lo que acaban de ver es, probablemente, uno de los fenómenos físicos más fácilmente reconocibles en nuestro diario vivir. Y es también la inspiración para el post de hoy, ya que el pasado 29 de noviembre fue el natalicio del físico-matemático austríaco Christian Doppler, a quien debemos este fenómeno que inspiró aquel triste disfraz que ocupa ese despreciable personaje de esa deplorable serie a la que no nos referiremos en este post.
Imagen no encontrada.
Doppler Begins
Christian Doppler nació en Salzburgo en 1803. Tras completar su educación escolar, Doppler dio la PSU del imperio austro-húngaro y le alcanzó justito para estudiar filosofía en Salzburgo, además de matemáticas y física en el Instituto Politécnico Real e Imperial (actual Universidad Técnica de Viena). En 1835 comenzó su trabajo en el Instituto Politécnico de Praga. Tan sólo un año después se hizo famoso (manteniendo las proporciones, claro) al descubrir que la frecuencia observada de las ondas de luz y de sonido eran afectadas por el movimiento relativo entre la fuente y el detector.
Christian Doppler
Aquí un retrato de Christian. Sospechamos que su eterna lucha contra la peineta lo motivó a estudiar todo tipo de ondas.
En 1842 Doppler dio una lectura en la Sociedad de Ciencias en Bohemia (República Checa, no confundir con la bohemia porteña). Doppler propuso este efecto en su tratado «Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels» («Sobre el color de la luz en estrellas binarias y otros astros»).
Una percepción aguda de los bajos
En 1845, Christophe Ballot, un meteorólogo danés (algo así como el Iván Torres de la época) realizó una demostración pública del efecto. Ballot vivía al lado de una línea del tren y notó el cambio de tono en los pitos y sonidos a medida que el tren pasaba. Moviendo algunos contactos, logró llenar un tren y el andén con trompetistas y los hizo tocar la misma nota mientras que el tren se movía a una velocidad de 65 km/h. Si bien los músicos en el andén se mantuvieron en la nota, los que iban en el tren se escuchaban con un tono un poco alto, el que bajó a medida que el tren pasaba la estación. Todas las personas que estaban presentes en la estación fueron testigos del cambio en el tono con el paso del tren, con lo que se reconoció públicamente una de las herramientas más útiles de la física.
Si Ballot hubiese sido chileno, el experimento sería más entretenido aún...
Con manzanitas, porfis
Para explicar el efecto Doppler, necesitamos partir con algunas características básicas del movimiento de ondas. Las ondas existen en distintas formas: en las ondulaciones en la superficie de una laguna, en los sonidos, en la luz, en los temblores, en el onda onda; además, todos estos fenómenos poseen un movimiento periódico.
Dos de las características comunes utilizadas para describir todos los tipos de movimiento ondulatorio son la longitud de onda y la frecuencia. Imaginemos una onda como una serie de cerros y valles. La longitud de onda corresponde a la distancia entre dos cimas consecutivas y la frecuencia es la cantidad de cimas que pasan a través de un punto de referencia en un periodo de tiempo dado.
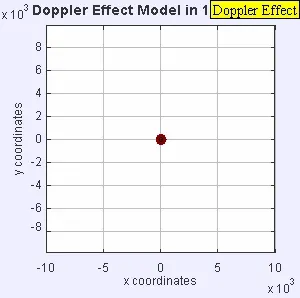
Imagine ahora que existe un generador de cerros y valles, desde el cual van saliendo de forma continua cerros y valles (obviamente). Si este generador está detenido en un punto (que, para que se vea aún más científico, llamaremos x=0) y nos situamos sobre él, veremos algo como la siguiente figura:
Generador de sonido estacionario. [1]
Para un observador situado en cualquier punto, el flujo de cerros generados —el «tren de ondas»— llegará con la misma frecuencia con la que fue emitido desde el generador. Tomando el ejemplo del experimento de Ballot, este caso corresponde a los músicos parados en la estación.
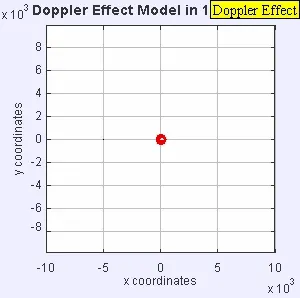
Si ahora montamos nuestro generador de ondas (o sea, cerros) en un vehículo y lo empezamos a mover a una velocidad constante, veremos algo similar a la siguiente figura:
El generador de ondas se mueve a una velocidad menor a la del sonido. [2]
A medida que el generador se mueve y continúa emitiendo ondas, la frecuencia con la que un observador recibirá el frente de la onda variará respecto de la posición en la que se encuentre. Podemos ver en la figura que si el generador se mueve hacia el observador (ubicado, por ejemplo, en x=10), la frecuencia aparente con la que recibe las ondas aumenta (o sea, sería un observador más ondero), mientras que para un observador ubicado en x=-10, la frecuencia aparente es menor a la emitida por el generador.
Ahora consideremos que nuestro generador de ondas emite ondas sonoras. ¿Qué pasa si la velocidad con la que movemos el generador es igual a la velocidad a la que se emite el sonido? Recordemos de nuestras clases de física en el colegio que la velocidad a la que se desplazan las ondas sonoras por el aire es de aproximadamente 340 m/s (alrededor de 1200 km/h). A medida que aumentamos la velocidad de movimiento del generador, nos acercaremos a un punto en que un observador ubicado en la dirección a la que se mueve el generador no recibe las ondas sonoras sino hasta que el mismo generador pasa por su posición.
El generador alcanza la velocidad del sonido. [3]
Finalmente supongamos que el generador se mueve a una velocidad superior a la del sonido, o a velocidad supersónica. Como podrán deducir de los casos anteriores, teniendo en cuenta que el generador se está moviendo a una velocidad mayor que la de las ondas que emite, irá por delante del tren de ondas, por lo que un observador estacionario verá pasar el generador y posteriormente oirá el sonido emitido por él.
El generador se mueve a una velocidad supersónica. [4]
Queremos destacar el comportamiento del fenómeno a velocidades supersónicas. El observador estacionario no recibirá ningún sonido hasta después de que el generador haya pasado por su posición. Cuando el generador pase justo por su lado, recibirá una explosión de sonido (sonic boom) y posteriormente oirá dos sonidos: el primero corresponderá a las ondas emitidas luego de pasar por su posición, a un tercio de la frecuencia original (algo así), y el segundo, más interesante, será el creado por las ondas antes de pasar por su posición, pero con una frecuencia negativa (bien mala la onda), es decir, lo escucharía al revés.
Bonito efecto, ¿pero pa’ qué sirve?
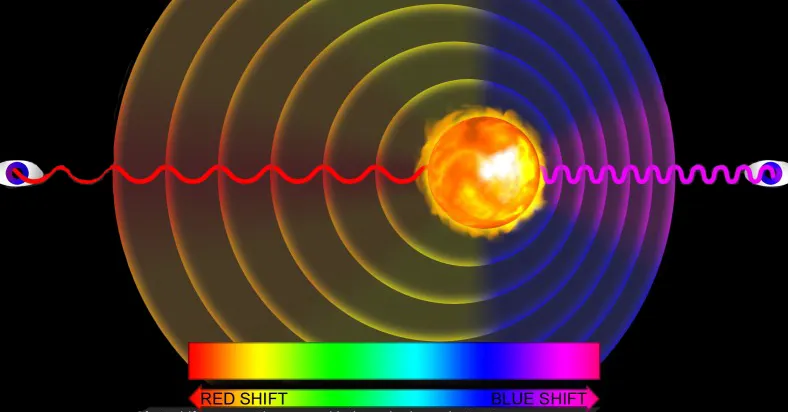
En el tratado que describió por primera vez el fenómeno, Doppler predijo que el efecto sería utilizado ampliamente por la astronomía. Su uso es directo en la medición actual de la velocidad con la cual estrellas o galaxias se alejan o acercan a la tierra mediante el cambio de la longitud de onda (del color) de la luz que llega a nuestros telescopios. Esto se llama corrimiento al rojo o redshift para los comunistas (?): si las estrellas se alejan de nosotros, la longitud de onda se hace más roja (longitudes de onda más grandes) y, si se acercan, más azul (longitudes de onda más pequeñas).
Hoy utilizamos el efecto Doppler en muchas interesantes aplicaciones. Por ejemplo, el radar Doppler usa microondas reflejadas para determinar la velocidad de movimiento de objetos distantes; en meteorología, el efecto se usa para caracterizar el movimiento de las nubes y los patrones de clima.
En medicina, el efecto Doppler se utiliza para obtener información sobre coágulos, arterias bloqueadas y funciones cardíacas en adultos y durante el embarazo (de hecho, el uso del efecto Doppler en embarazos se encuentra ampliamente difundido por ser confiable y no invasivo). ¿Y cómo se puede hacer esto? Emitiendo ondas de ultrasonido que rebotan contra los órganos y estructuras que se están estudiando. A medida que los ultrasonidos avanzan por el cuerpo, sufren atenuación, dispersión y reflexión dependiendo de las propiedades físicas de las estructuras que encuentran a su paso. Así, cuando las ondas regresan al aparato, son interpretadas por una computadora y transformadas en imágenes.
En resumen, nuestro entendimiento del efecto Doppler nos ha permitido aprender más sobre el universo del que somos parte, medir el mundo en el que vivimos y mirar el interior de nuestros cuerpos sin abrirlo (lo que debe haber dejado sin trabajo a varios cirujanos...). Mientras tanto, futuras aplicaciones apuntan a una mejor navegación computarizada y hasta «revertir» el efecto, lo que nos podría llevar al desarrollo de capas de invisibilidad. Chúpate esa, Harry Potter.