DOBBLE: Un juego de mesa que esconde un tesoro matemático

El post de hoy es obra del Colectivo MateMaNiA2, y si bien originalmente no fue pensado para la situación actual, es sin duda un excelente juego matemático para estos días de aislamiento.

«Todo a tu alrededor es matemáticas», decía Shakuntala Devi, célebre escritora india que ostentaba varios récords mundiales de cálculo mental. En efecto, hay matemáticas en las leyes de la naturaleza, en las finanzas, en el movimiento de las personas…

Pero, ¿puede haber matemáticas en un juego de mesa?

Ciertamente: el ajedrez es un ejemplo claro de esto. Pero también hay matemáticas en otro juego, mucho más sencillo, que se ha vuelto muy popular en los últimos años: el Dobble.

¿En qué consiste este juego? Un mazo de 55 cartas, cada una consta de ocho figuras que vienen dispuestas cuidadosamente en cada carta de modo de satisfacer la siguiente premisa fundamental:

HAY DOS CARTAS QUE TIENEN EXACTAMENTE UNA FIGURA EN COMÚN

Por ejemplo, en la imagen de portada, las cartas de la izquierda coinciden en el signo de interrogación, las de arriba en el ancla y las de abajo en el payaso.

En la variante más clásica del juego, las cartas se reparten en igual cantidad entre los jugadores y se deja una al centro de la mesa. Quien identifica más rápido la figura en común entre la carta de la mesa y la primera carta de su mazo deja esta sobre la mesa (encima de la anterior) y pasa a la siguiente. La acción continúa igual: se desprende de una carta quien identifica más rápido la figura en común entre la nueva carta de la mesa y la primera de su mazo… Hasta que alguien consigue deshacerse de todas sus cartas y, con ello, ¡gana la partida!

Fácil, bonito, simpático y, sobre todo, muy entretenido. Pero, por simple curiosidad, nos preguntamos cómo se determinó qué figuras debían ir en cada carta del juego para satisfacer la premisa fundamental y, con ello, se pueda jugar.

En realidad, no es nada sencillo.

Una idea geométrica

Supongamos que trazamos varias rectas en el plano, todas con direcciones diferentes, de modo que dos cualesquiera de ellas se intersectan.

Si en cada punto de intersección dibujamos una figura a nuestro gusto (todas las figuras deben ser diferentes), entonces podemos fabricar un juego de cartas que satisface la premisa fundamental de la manera siguiente: cada carta corresponde a una de las rectas trazadas y en ella incluimos las figuras dibujadas sobre los puntos de intersección de dicha recta con alguna otra. ¡Hemos fabricado un juego de Dobble!

El problema es, sin embargo, evidente: se usan demasiadas figuras en cada carta. Y, cuando hay demasiadas figuras, estas se vuelven cada vez más ilegibles. ¿Habrá una manera de usar menos figuras sin disminuir el número de cartas? Para lograr esto, intentaremos que una nueva premisa (a la que llamaremos complementaria) se satisfaga: 

PARA CADA PAR DE FIGURAS, EXISTE EXACTAMENTE UNA CARTA QUE LAS CONTIENE

En el ejemplo de la figura anterior, solo habría una carta que contenga la luna y el corazón al mismo tiempo. Aunque en otra carta la luna podría aparecer junto al rombo, por ejemplo.

Esta nueva premisa hace disminuir mucho la cantidad de figuras, pues, si hubiese muchas, entonces habría también muchas cartas.

El problema que nace ahora es el siguiente: es imposible trazar una cantidad finita (mayor que tres) de rectas en el plano de modo que: 

• dos cualesquiera de ellas se intersequen;
• dados dos puntos de intersección entre las rectas trazadas, otra de las rectas trazadas pasa por ellos.

Haga unos dibujos para convencerse de esto (luego trataremos de explicar por qué es verdad).

Un lugar donde todas las rectas se intersecan

Uno de los problemas con nuestra analogía geométrica es que en el plano existen rectas «paralelas», es decir, rectas que tienen la misma inclinación y que, por lo tanto, no se intersecan.

¿Habrá algún lugar donde todas las rectas se intersecan?

¡Por supuesto! ¡Nuestro planeta Tierra! Esto solo si lo consideramos esférico y no adscribimos a la creencia de que la Tierra es plana, claro está.

Obviamente, aquí no hay «rectas», pero las curvas que cumplen este rol son los «ecuadores», es decir, las grandes circunferencias que dividen a la esfera en dos mitades idénticas.

Estas son las trayectorias que debiera, por ejemplo, seguir un avión para viajar de un punto a otro. ¿Por qué? Pues porque son las que recorren la menor distancia entre dos puntos: por ello son llamadas «geodésicas».

Evidentemente, cualquier par de ecuadores de una esfera se intersecan. El problema es que la intersección es doble: aparece un punto simultáneamente con su «antipodal». ¿Qué hacer? Simple: pensaremos que un punto sobre la esfera y su opuesto son el mismo. ¿Raro? Puede ser. El objeto que consideramos ya no es una esfera, sino tan solo un hemisferio, con la salvedad de que incluso a lo largo del ecuador que lo delimita debemos identificar cada punto con su opuesto. Este objeto, que no es tan sencillo de visualizar (pues lleva incorporada la famosa cinta de Möbius), es fundamental para nuestro juego.

Finitas rectas

Tenemos un problema inmenso aún, pues hay una infinidad de ecuadores: ¿cómo sabemos cuáles elegir? 

A decir verdad, no vamos a elegir ninguno de ellos, sino que cambiaremos (otra vez) de mundo y los ecuadores de este nuevo mundo servirán. Para esto, señalemos que todo lo descrito anteriormente se puede reescribir en lenguaje algebraico, con hermosas fórmulas que evitaremos reproducir aquí para no espantar a nadie.

Estas ecuaciones tienen lugar en el famoso campo de los números «reales» que aprendemos en la escuela. Pues bien, lo que haremos es cambiarlo por un sistema numérico finito. Se trata de un mundo de solo unos cuantos números en el que podemos sumar, restar, multiplicar y dividir (nunca por cero) conservando todas las bonitas propiedades conocidas (como esa que dice que «el orden no altera el producto», pedantemente llamada «conmutatividad»).

¿Un ejemplo? Piense en un reloj (antiguo, de esos con manecillas). Cuando marca la hora, este va desde $0$ a $11$ y, al llegar a $12$, vuelve a $0$. Es como si el $12$ se fundiera con el $0$, con lo cual quedan apenas $12$ números $(0, 1, 2, … , 11)$. Esto es lo que se conoce como la «reducción módulo $12$». En esta aritmética, la suma $8+7$ ya no es $15$, sino $3$ (si salimos de viaje a las $8$ y nos demoramos $7$ horas en el trayecto, entonces llegaremos a las $3$). También podemos multiplicar: por ejemplo, $5 \times 4 = 8$.

A decir verdad, el $12$ no es muy buen número por la razón siguiente: $4 \times 3$ es igual a $12$, que se identifica con $0$. El punto es que hemos aprendido en la escuela (y desearíamos que siga siendo cierto) que para fabricar el $0$ en una multiplicación, uno de los factores debe ser $0$, y aquí ni $3$ ni $4$ son $0$.

Para seguir respetando esta propiedad fundamental de «ausencia de factorización de $0$» debemos «volver al inicio» en un instante que sea un número primo (es decir, que no tenga divisores, salvo $1$ y sí mismo). Si este es el caso, conseguimos hermosas tablas de suma y multiplicación que respetan todas nuestras queridas propiedades de la escuela. He aquí las tablas de los números «módulo $7$»:

Ya, todos estos números y tablas parecen muy bonitos, pero… ¿cómo diantres se fabrica el Dobble?

Se toman todas las fórmulas de las que hablamos arriba pero que evitamos escribir. Luego, en lugar de leerlas sobre los números reales, las leemos en esta aritmética módulo $7$ y consideramos todos los «ecuadores» posibles. ¡La solidez de la construcción permite que las dos premisas se cumplan simultáneamente!

Obviamente, podría hacerse lo mismo con otros números primos. Le dejamos como ejercicio hacer todo reduciendo módulo $11$: ¡podría crear un juego con muchas más cartas!

El enigma de las dos cartas perdidas

El extraño espacio a partir del cual fabricamos nuestro Dobble tiene un nombre en matemáticas: plano proyectivo finito. ¿Cuántos puntos tiene? Para contarlos, recuerda que nuestro espacio es como un hemisferio con un ecuador de puntos opuestos identificados… solo que ahora esto debe ser pensado en la aritmética finita correspondiente (construida con un número primo p). Con paciencia, se constata que:

• el hemisferio consta de $p^2$puntos, que corresponden a los pares de la forma $(a,b)$, con $a$ y $b$ entre $0$ y $p – 1$; 
• en el ecuador hay otros $p + 1$ puntos.

Así, en total, hay $p^2+p+1$ puntos. Por ejemplo, para $p=7$ resultan $7^2+7+1$ puntos, es decir, $57$. Compruébalo: ¡Hay $57$ dibujos distintos en el juego de Dobble!

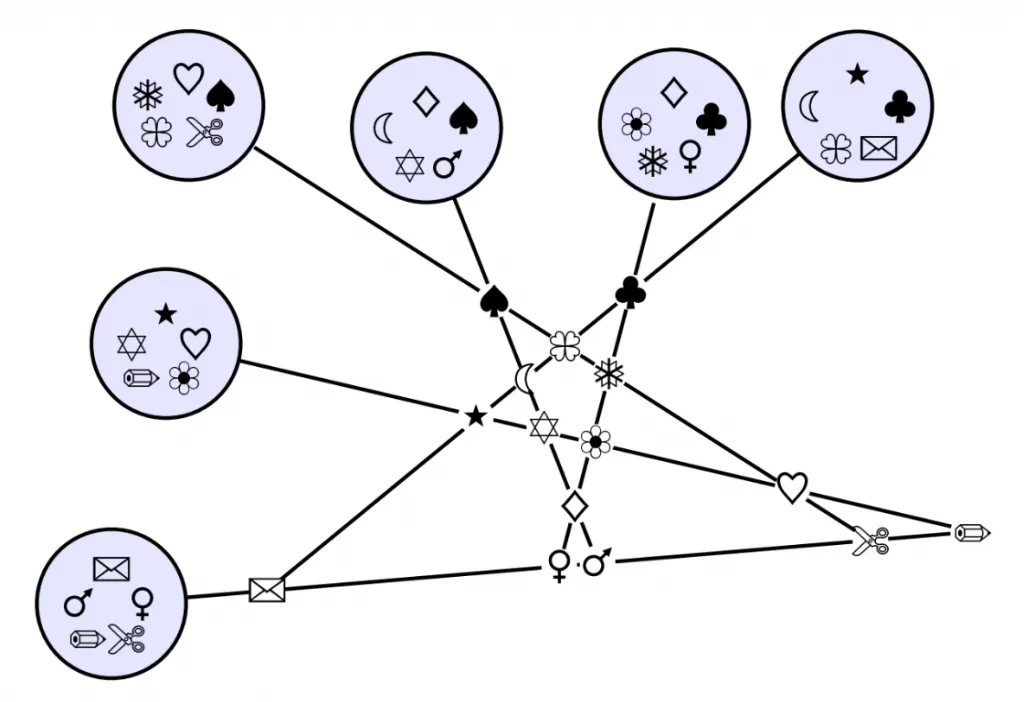
¿Y cuántas rectas hay? Pues bien, la premisa fundamental es tan similar a su complementaria (en matemáticas se dice que son “duales” una de la otra) que es natural esperar que haya la misma cantidad de rectas que de puntos. Sin embargo, ¡el Doble tiene $55$ cartas, y no $57$! Rarísimo: por alguna razón desconocida, los creadores del juego decidieron suprimir dos cartas. Nosotros las hemos recuperado: si no nos crees, toma tu juego de Dobble y constata que las dos cartas de abajo siguen satisfaciendo las premisas con todas las tuyas… 

Bonus track para valientes

Quienes son adictos al Dobble saben que hay otra variante del juego: la de los tríos. En esta, un “administrador” comienza disponiendo $9$ cartas sobre la mesa, y las restantes se reparten entre los jugadores. Quien encuentra primero tres cartas en las que se repite una misma figura las coge para sí, y el administrador coloca tres nuevas cartas en la mesa. El juego continúa así hasta que se agota el mazo (al final puede que no haya tríos, así que las últimas cartas se las queda quien robó la última vez). Gana quien logra acumular más cartas.

¿Por qué funciona esta variante? Porque siempre que se juntan $9$ cartas habrá un trío. ¿La explicación? Bueno, se puede razonar “a fuerza bruta”: forma todos los grupos posibles de $9$ cartas y corrobóralo. El único problema con este método es que, con $55$ cartas, hay $\frac{55 \times 54 \times 53 \times 52 \times 51 \times 50 \times 49 \times 48 \times 47}{1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8 \times 9} = 6358402050$ posibilidades, por lo que te tomará varias vidas verificarlo (aunque con un computador podrías trabajar más rápido…). Otro método: piensa… (advertencia: la explicación no es tan sencilla).

Para jugar

Si quieres seguir jugando puedes crear tus propios juegos usando la aritmética módulo $2, 3, 5, 7, 11, 13,$ etc. En particular, con $p=11$, crearás un juego de $11^2+11+1=133$ cartas. ¡Con este podrás invitar a más gente a la diversión! Si tienes problemas con la confección puedes consultarnos. Nosotros hemos codificado algunos de los espacios descritos más arriba; en particular, reproducimos un juego completo para $p=7$ (esto es, de $57$ cartas), al que hemos colocado figuras alusivas a la explosión social y hemos llamado Yo Apruebo + (¿por qué será?). 

¡A votar! 

Perdón: ¡A jugar!