Probablemente usted ha intentado envolver una pelota en papel de regalo. Aunque es posible lograr que se vea bastante bien, ni siquiera el empaquetador con más propinas puede evitar que el papel quede con algunas arrugas o dobleces (sobre todo si son scouts). ¿Habrá alguna forma de hacerlo perfectamente, sin romper el papel?
Disclaimer: Igual para envolver una pelota es mejor usar una caja, puesto que el regalo será obvio si se usa un papel. Sí, papá, siempre lo supe. Mi cara de sorpresa fue una actuación.
Este problema se puede plantear de una forma recíproca, pero a fin de cuentas equivalente: ¿es posible aplanar perfectamente una cáscara de naranja sin romperla?
La respuesta a ambas preguntas es «no» y no es porque seamos demasiado torpes para hacerlo: es matemáticamente imposible hacerlo. Aunque pueda parecer sorprendente, este hecho repercute de forma significativa en nuestra vida cotidiana, con consecuencias mucho más trascendentales que no poder aplastar una naranja. En efecto, no es posible «aplanar» la Tierra en un mapa cuadrado sin romperla ni estirarla. Los mapas que usamos todos los días necesariamente incluyen distorsiones indeseables.
Vamos a leer un poco sobre las
propiedades matemáticas que impiden hacer mapas perfectos y luego vamos a hablar sobre cómo cresta se las han tratado de arreglar para hacer mapas de todas formas a pesar de estas limitaciones.
De hecho, es muy probable que si el trovador (?) Ricardo Arjona hubiese leído este post, su canción diría algo como «Olvidarte es más difícil que planchar un mapa» (aunque seguiría siendo igual de mala).
Me fascina tu curvatura
La respuesta negativa a las preguntas anteriores se basa en la curvatura: un concepto matemático que mide qué tanto se aleja una superficie de ser un plano en un punto dado.
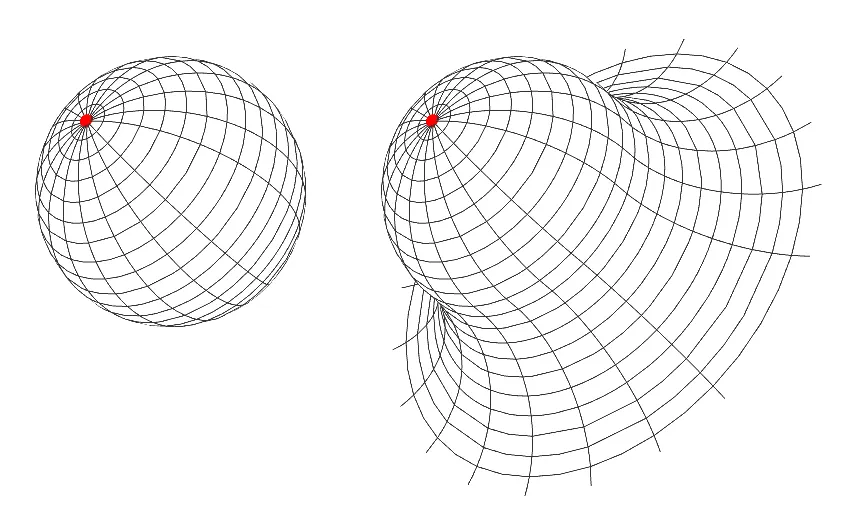
Cada punto sobre la superficie tiene asociado un número, la curvatura de ese punto, que mide qué tan «poco plana» es la superficie vista desde ese punto. La curvatura es una noción local, lo que significa que sólo depende de las cercanías del punto y no de toda la superficie.
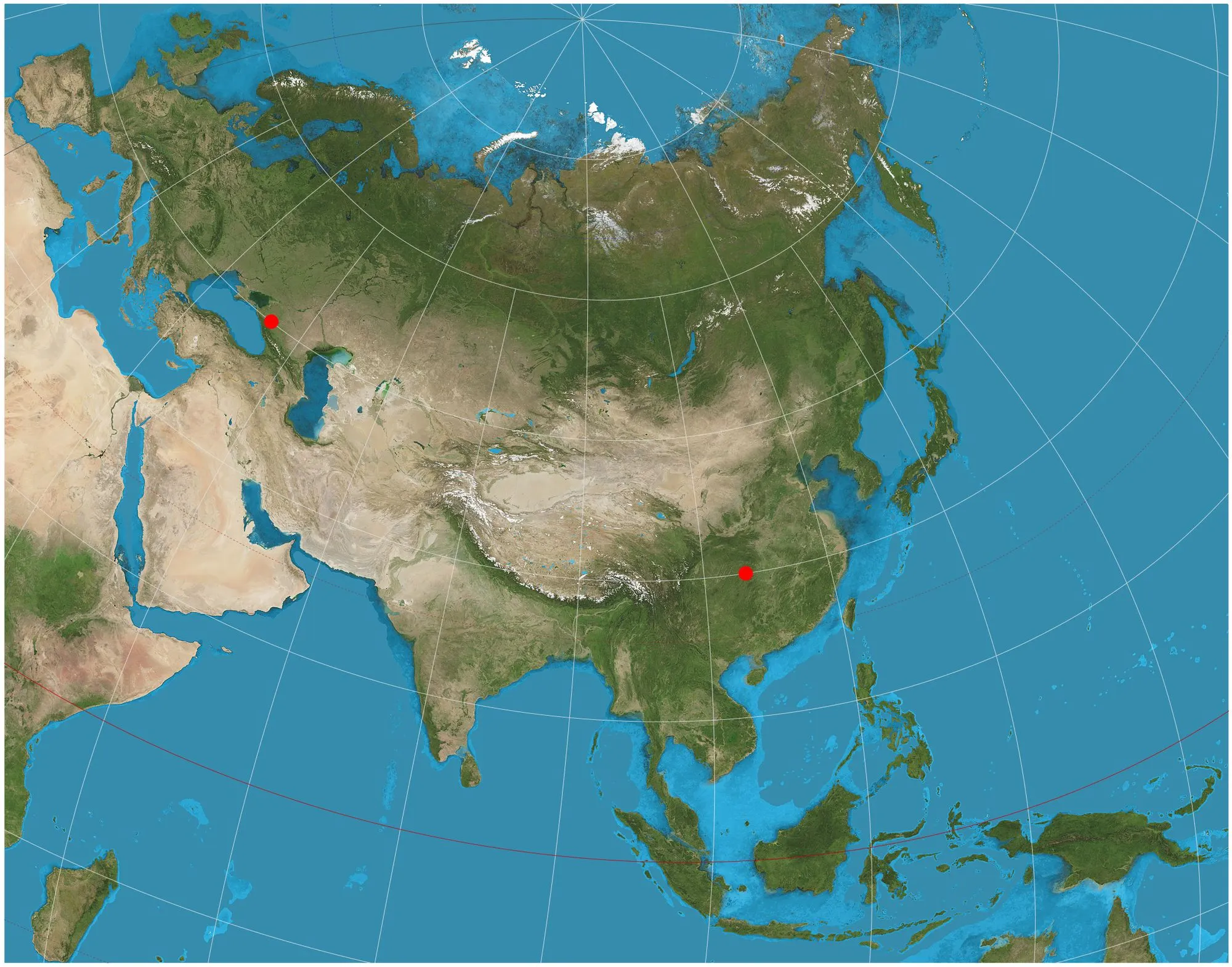
Ambas superficies tienen la misma curvatura en el punto rojo, pues son iguales alrededor de ese punto. Claramente, las superficies no son globalmente iguales.
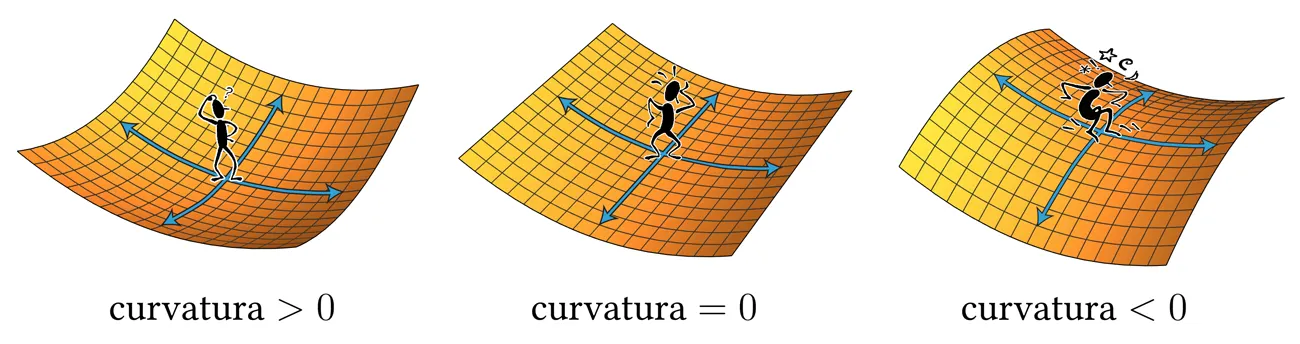
El signo de la curvatura (es decir, si es positiva, negativa o cero) se puede interpretar fácilmente, como muestra la siguiente imagen:
Curvatura positiva: la superficie es curva en ambas dimensiones. Van en el mismo sentido. Curvatura cero: la superficie es plana en al menos una dimensión. Curvatura negativa: la superficie es curva en ambas dimensiones. Van en sentidos opuestos.
Los matemáticos, que obviamente no tienen nada mejor que hacer, han logrado entender cuáles son las superficies que tienen curvatura constante, es decir, que es igual en todos sus puntos. Dependiendo de si la curvatura es positiva, cero o negativa, respectivamente, toda superficie
con curvatura constante proviene de una de las siguientes tres superficies fundamentales: la esfera, el plano y el hiperboloide [1,2].
Un hiperboloide hecho de lana. El hiperboloide es la menos conocida de las tres superficies fundamentales con curvatura constante. Su curvatura es negativa e igual en todos los puntos. Fuente: Wikipedia.
¿Y qué tiene que ver esto con los mapas, los regalos o las naranjas?
Fue Carl Friedrich Gauss, uno de los más grandes matemáticos de todos los tiempos, el que logró establecer en su Theorema Egregium (latín para «Teorema destacable») que la curvatura no cambia al deformar una superficie sin romperla ni estirarla [3]. Sabemos que una esfera tiene curvatura positiva y que un plano tiene curvatura cero, por lo que es imposible transformar una esfera en un plano… A menos que estemos dispuestos a romperla o estirarla. Esto nos entrega la respuesta negativa al problema de envolver una pelota, aplastar la cáscara de una naranja o diseñar un mapa perfecto.
Se pueden obtener más conclusiones interesantes de este teorema. Por ejemplo, un cilindro tiene curvatura constante igual a cero, pues se puede obtener doblando un rectángulo plano.
Piense usted en la curvatura del cilindro cuando se encuentre con el rollo de papel higiénico vacío en la casa de sus suegros.
Soy el mapa, soy el mapa
«A ver, a ver, momentito, momentito. Ya están mintiendo de nuevo: ¿cómo dicen que los mapas no existen, si tengo uno acá en mi pieza?» Buena pregunta. La discusión anterior uestra que no es posible transformar perfectamente una esfera en un plano, pero sí es posible hacerlo si estamos dispuestos a perder algo. Estas transformaciones se llaman proyecciones.
¿Perder qué, exactamente? Bueno, depende. Si queremos un mapa perfecto, alguien podría decir que se tienen que mantener las distancias entre todo par de puntos (importante para hacer viajes), los ángulos entre cada tres puntos (importante para la navegación en el mar) o las áreas de cada país (importante para no herir susceptibilidades patrióticas de países en vías de desarrollo).
Sin embargo, el theorema egregium de Gauss echa por tierra estos requerimientos: ¡no se pueden tener todos a la vez! Hay que conformarse con tener algunas características y desechar las otras.
Proyección de Mercator
La proyección de Mercator es la más usada actualmente. Lleva su nombre debido al cartógrafo flamenco Gerardus Mercator (de la región de Flandes de la actual Bélgica: no, no es ningún animal), quien la desarrolló en 1569. Su objetivo era claro: la navegación.
La principal característica de la proyección de Mercator es que las loxodrómicas de la Tierra pasan a ser líneas rectas en el mapa.
¿Loxoqué?
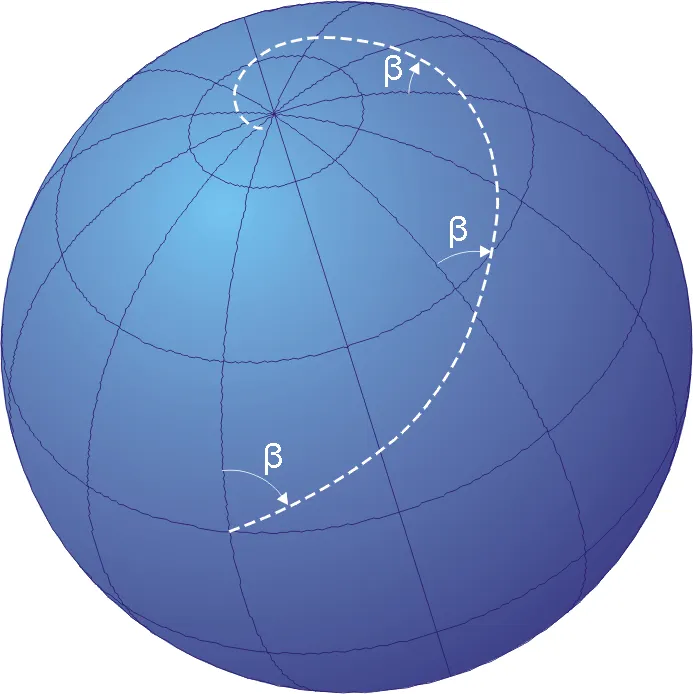
Las loxodrómicas (del griego para «curso oblicuo») son las curvas que se producen al seguir una dirección fija de una brújula. Se puede trazar una loxodrómica entre dos puntos cualesquiera y ésta
siempre cortará a todos los meridianos con el mismo ángulo.
Ejemplo de una loxodrómica. Fuente: Wikipedia.
Por lo tanto, para seguir una línea recta en un mapa de Mercator basta seguir una dirección fija de la brújula. ¡He ahí por qué resultó tan útil para la navegación!
Esta proyección preserva los ángulos, es decir, el ángulo entre dos líneas en la tierra es el mismo en el mapa. Además, preserva más o menos bien las áreas de las regiones pequeñas, pero las regiones grandes se ven muy distorsionadas.
Mapa de Mercator de la Tierra. Notar que la Antártida parece ser gigantesca, mucho más grande que África. En realidad, ¡África es más de dos veces más grande que la Antártida! Fuente: Wikipedia.
Para peor, la distorsión se hace cada vez más aberrante en la medida que nos alejamos del Ecuador y nos acercamos a los polos. Esto hace que, por ejemplo, Groenlandia se vea del mismo tamaño de África, cuando en realidad tiene un área… ¡Catorce veces más chica!
Si le interesa ver cuánto es capaz de deformar el mapa de Mercator, en la página The True Size podemos comparar, moviendo en el mapa, los tamaños «verdaderos» de un país frente a otro.
Esta deformidad no ha evitado la popularidad del mapa. La mayoría de los servicios en línea de mapas, incluyendo Google Maps, usan una variación de la proyección de Mercator (llamada Web Mercator), adaptada levemente para permitir el zoom hasta el nivel de ciudad.
Otros mapas
¿Y qué cosa existe aparte de Mercator? Hay más proyecciones que pokémones. Vamos a hacer una revisión rápida por muchos tipos de proyecciones para ver la variedad y deformidad que pueden llegar a tener.
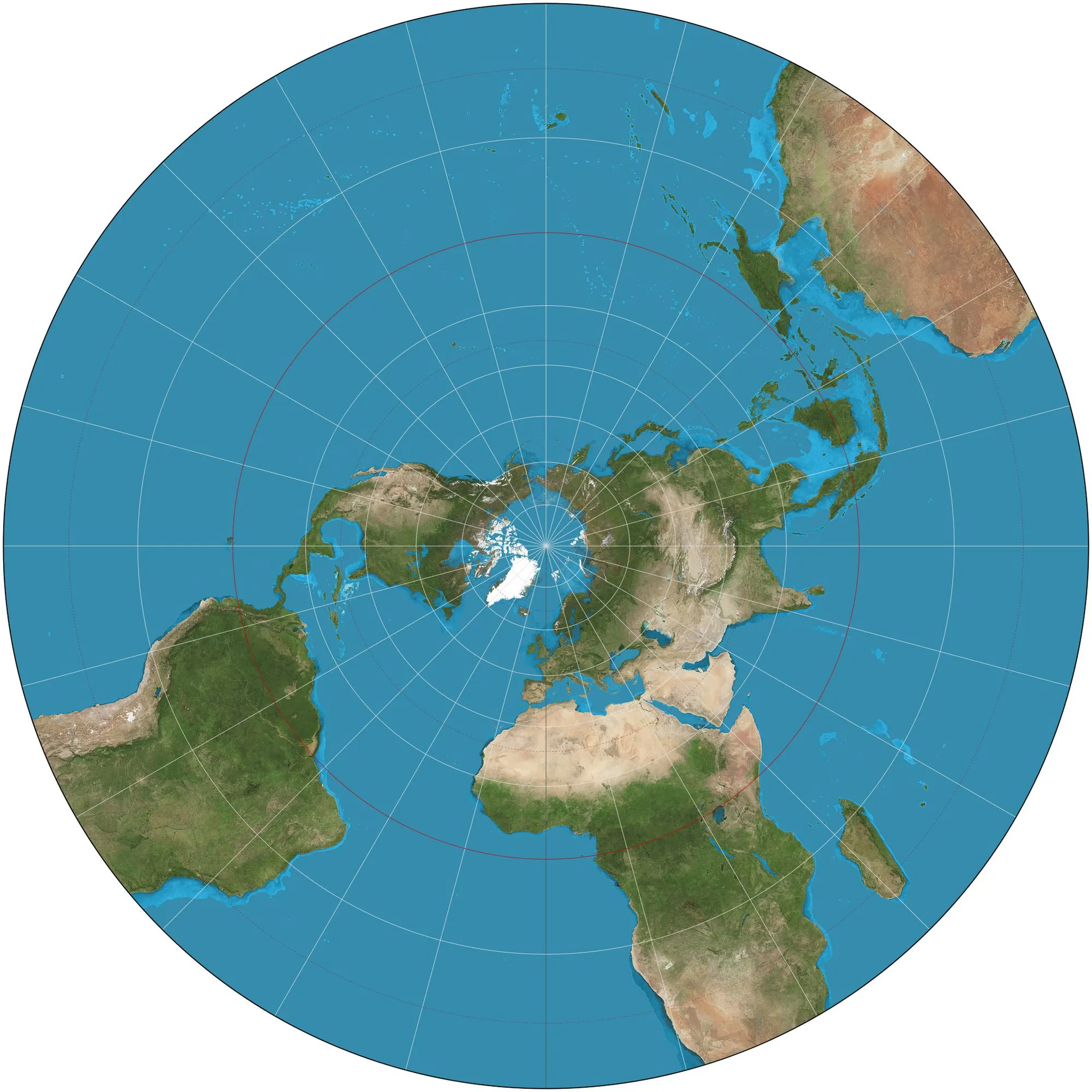
Otra proyección que preserva el ángulo, igual que la Mercator, es la proyección estereográfica. Esta proyección se hace a partir un punto (típicamente, uno de los polos). Tiene la propiedad de que preserva ángulos, los paralelos (como la línea del Ecuador) quedan como círculos concéntricos y los meridianos (que van de norte a sur) quedan como líneas rectas. Al final de todo, queda algo parecido al logo de la ONU. Por motivos técnicos, sólo son buenos para visualizar un hemisferio de la tierra a la vez.
Proyección estereográfica de la Tierra. Una gran ventaja de esta proyección es que el mapa no muestra la ciudad de T A L C A. Fuente: Wikipedia.
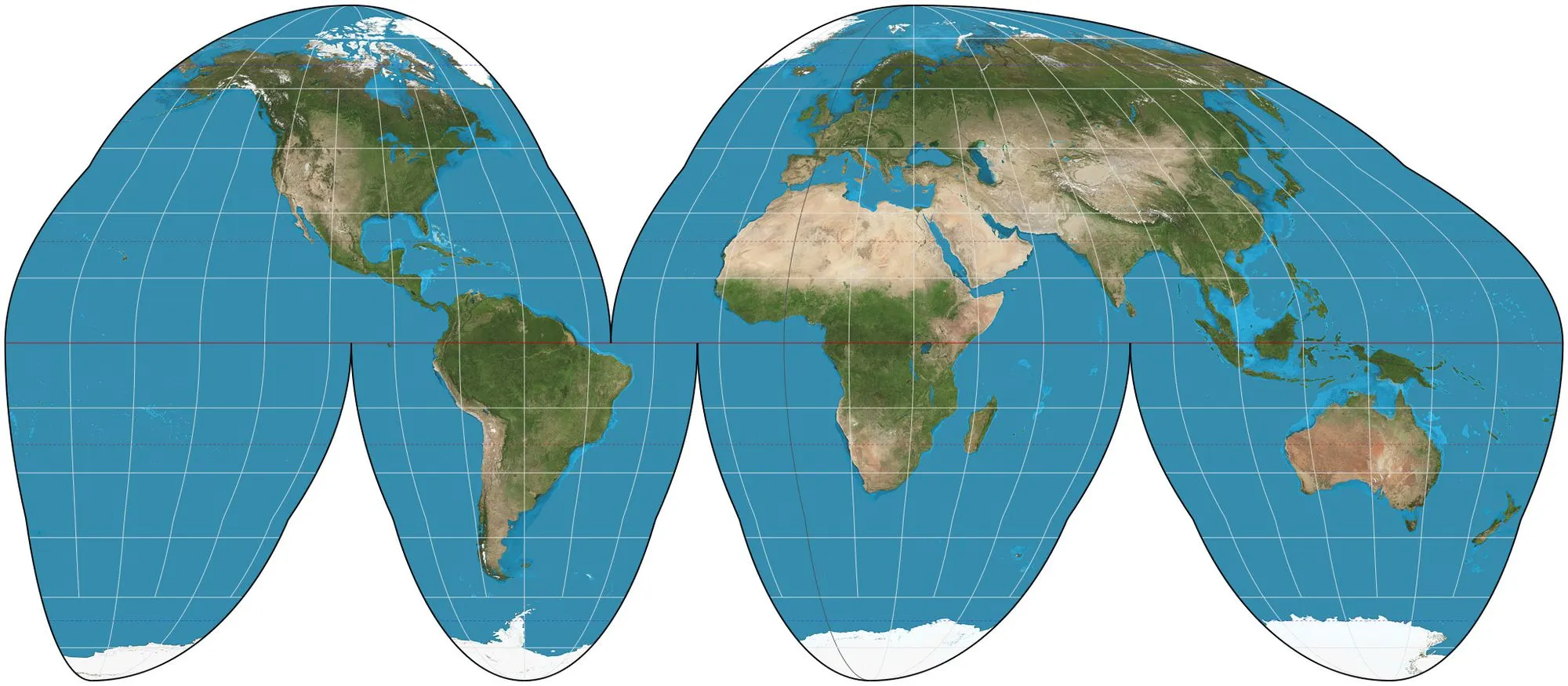
Una proyección que preserva el área en lugar del ángulo es la proyección de Goode. Además esta proyección trata de no deformar mucho la forma de los continentes con respecto a la de Mercator. El precio a pagar es que el mundo ya no se extiende de manera rectangular sino que tiene muchos «cortes».
Proyección de Goode, para los que no se quieren hacer problemas. Fuente: Wikipedia.
Supongamos ahora que no nos interesa preservar ángulo ni área, sino que distancia. Es imposible hacer un mapa que preserve la distancia entre todo par de puntos, pero se pueden hacer alguna clase de concesiones: a) preservar la distancia desde un punto fijo a todo el resto; b) preservar la distancia desde dos puntos fijos a todo el resto; o c) preservar la distancia entre meridianas.
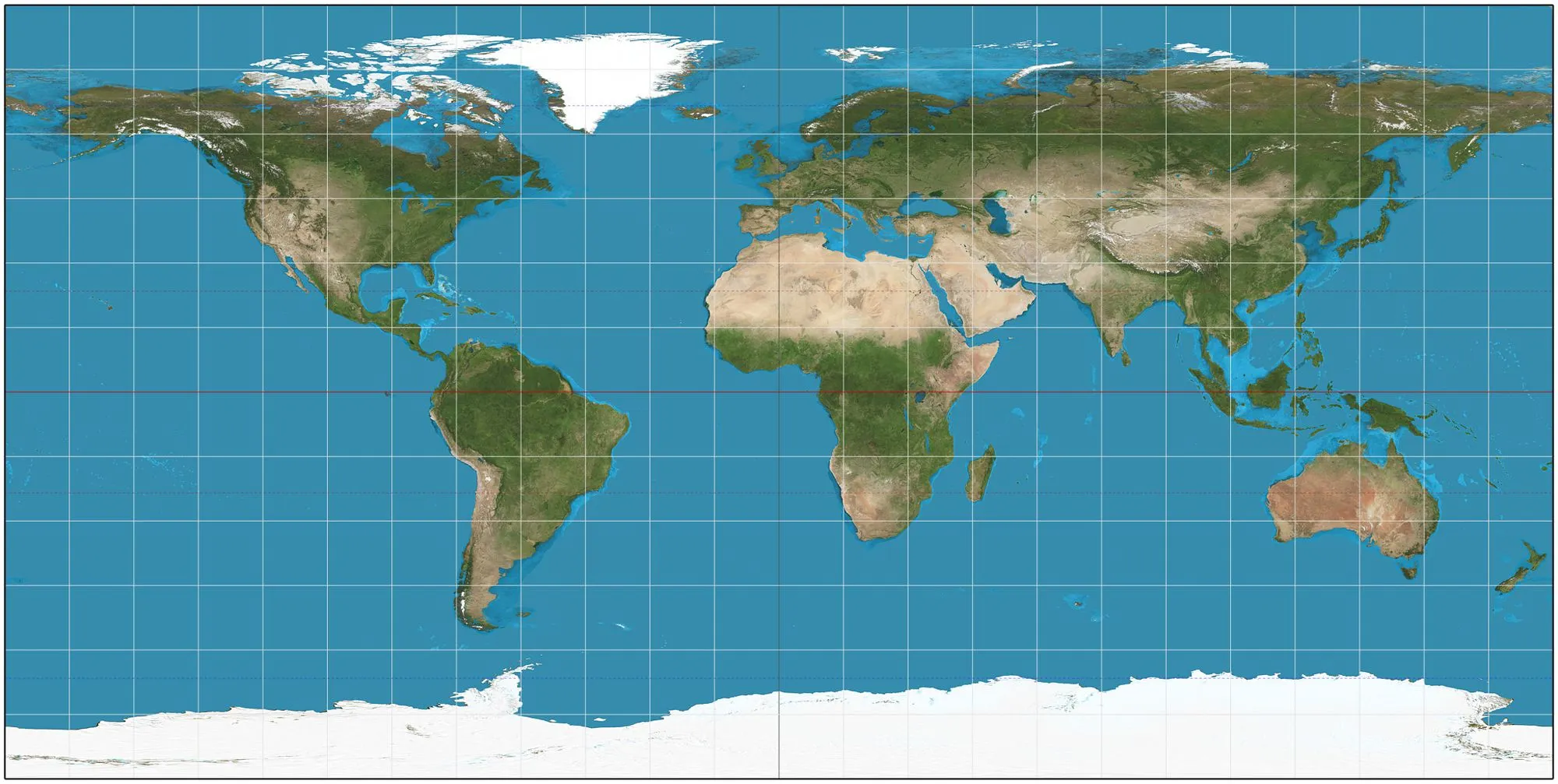
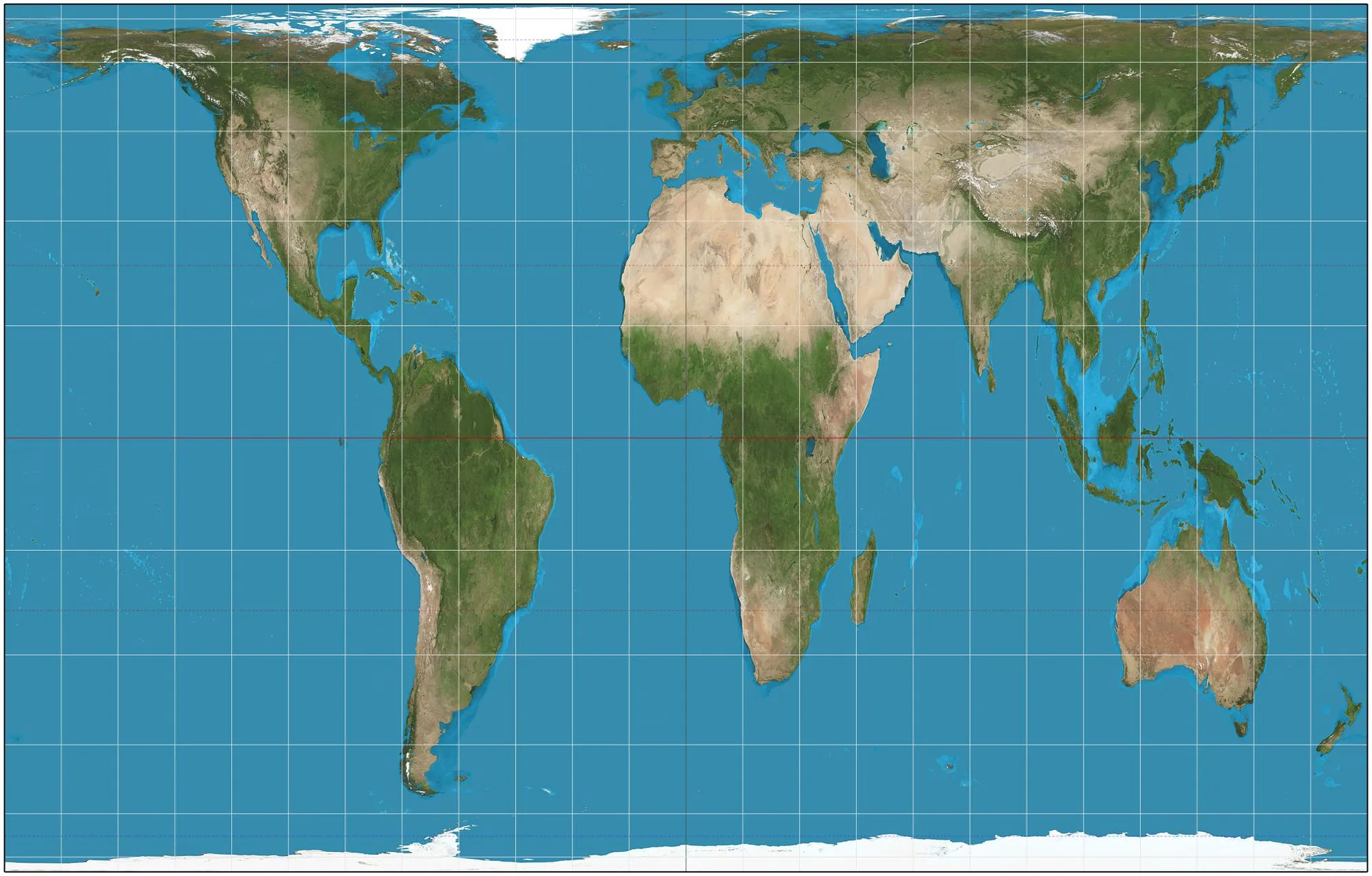
Una proyección que destaca por su simpleza es la proyección plate carrée (francés para cuadrada plana»), que es de especial importancia en computación, pues corresponde de manera directa los pixeles en ambas direcciones con las latitudes y longitudes.
Fuente: Wikipedia.
Fuente: Wikipedia.
La rarísima proyección retroazimutal de Hammer preserva las distancias proporcionales y las direcciones hacia un punto dado, pero a costa de deformar enormemente la forma del mapa.
De hecho la proyección se traslapa sobre sí misma, por lo que es necesario separar el mundo en dos mitades para verlo en un plano, que se ve más o menos así:
Estaban fuertes los cogollos, hermano. Fuente: Wikipedia.
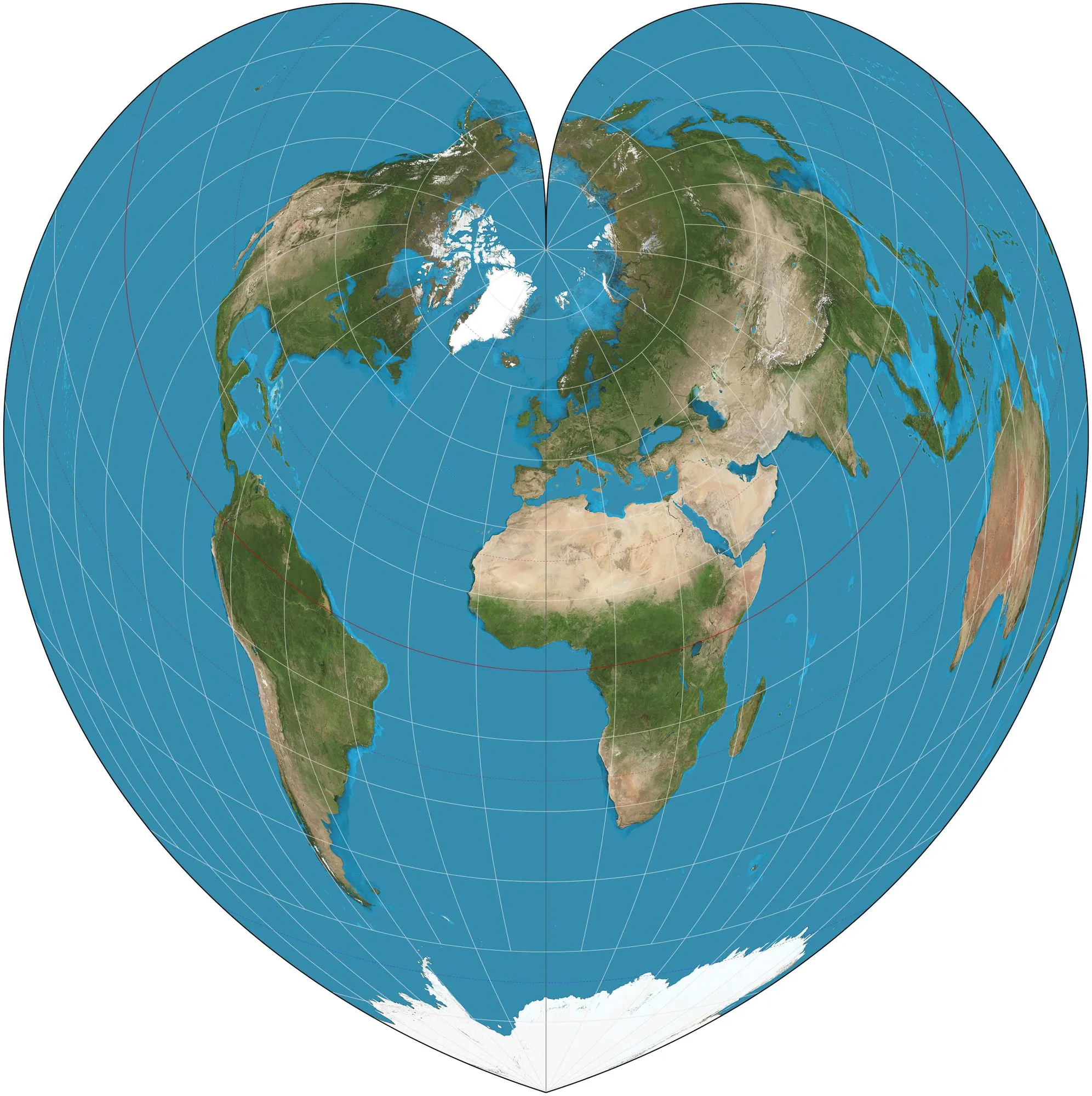
Y la proyección de Werner preserva la distancia hacia un punto (en este caso, el Polo Norte) a costas de deformar fuertemente las formas de todo el mapamundi. Pero debemos decir que el planeta adquiere una forma muy romántica. <3
El amor hace al mundo girar. Fuente: Wikipedia.
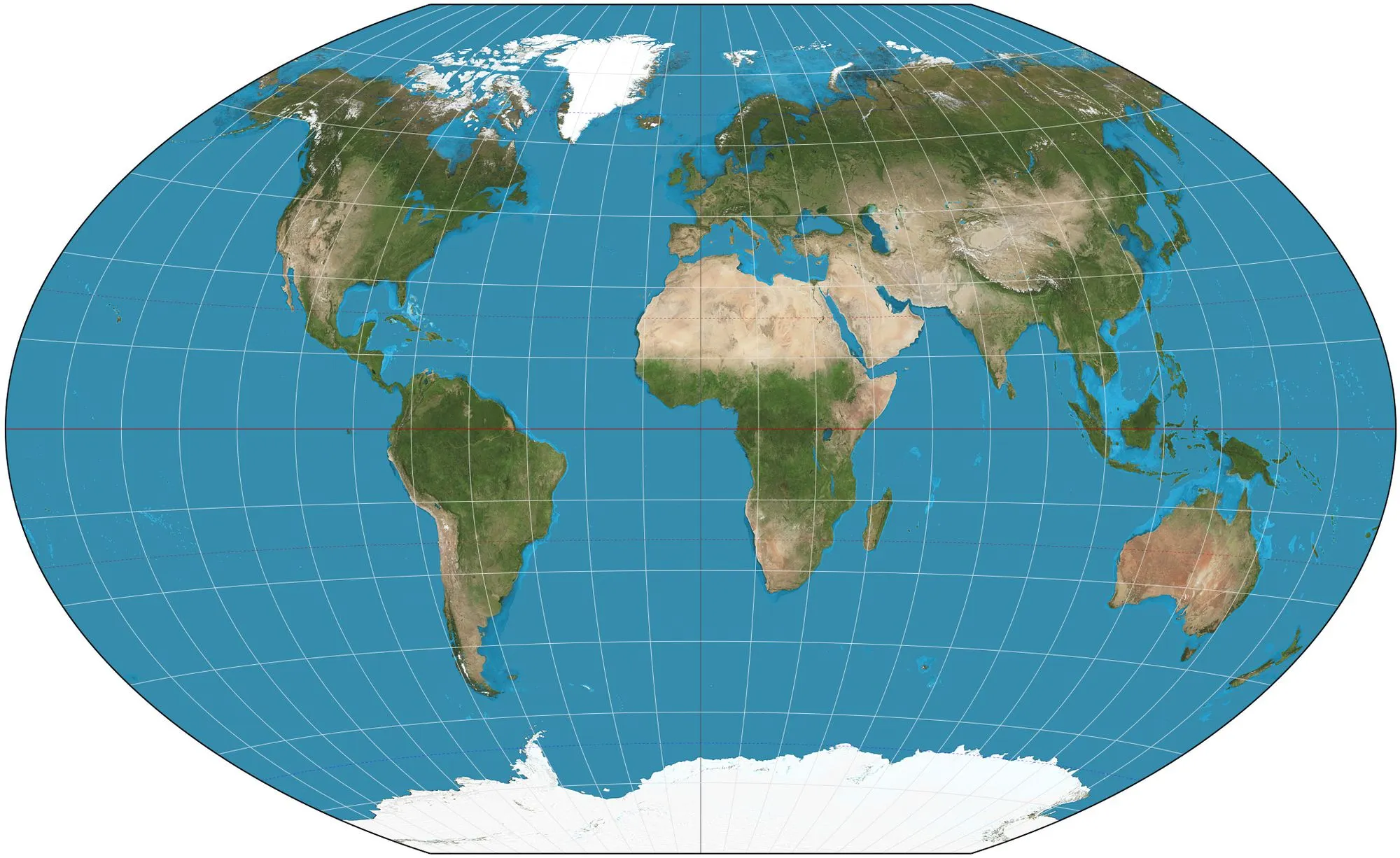
Una de las soluciones más elegantes es la proyección Winkel tripel. Es lo que salió cuando pensaron: «OK, no podemos preservar área, distancia y ángulo a la vez. Busquemos algo que no preserve nada, pero que haga que el mapa se vea lo mejor posible». Así, la proyección de
Winkel busca minimizar la tres distorsiones más importantes (área, dirección y distancia) encontrando un equilibrio entre las tres. Es la preferida, por ejemplo, por la asociación de la National Geographic.
Fuente: Wikipedia.
Ya, ¿y cuál mapa es el más bueno, entonces?
Aquí le debemos prestar ropa al vilipendiado Mercator. Su mapa no es maligno ni malvado.
No representa fielmente el mundo, pero a) nunca fue ése su objetivo —el cual era ser útil en la navegación y eso lo logra de manera excelente—, y b) es imposible que cualquier mapa pueda representar el mundo de manera fiel.
Esto no ha evitado que algunas personas con afán mercantilista hayan promocionado su propia versión del mapa diciendo que es la mejor «para enseñar». Peters, un hombre con mucha habilidad de convencimiento, propuso y promovió su versión del mapa anteriormente propuesta por Gall. La proyección de Gall-Peters ha sido promovida con un fin político: a diferencia de los mapas más conocidos, este no «favorecería» a ningún país cercano al Polo Norte agrandando su tamaño, por lo que sería más «igualitario», escapando del eurocentrismo (no del Eurocentro).
Fuente: Wikipedia.
Las críticas al mapa de Gall-Peters son muchas y de diferente estilo. A pesar de mantener el área
proporcional en cada país, estira los países ubicados cerca del Ecuador… dejando Europa y Norteamérica con sus proporciones casi intactas. Para ser un mapa en contra de la «desigualdad», es muy eurocentrista. Esto no ha evitado que sea promovido por instituciones por la UNESCO o diversas ONG que claman haber encontrado la proyección más justa e igualitaria del planeta, que, como vimos, es imposible que exista.
Pero en fin. Cada mapa preserva algunas características y, forzosamente, debe perder otras. Cada uso diferente tiene un mapa que le calza mejor. Nos quedamos entonces con la conclusión más demócratacristiana posible: el mejor mapa es el que sea mejor en ese caso. La matemática lo quiso así.
NB: Si usted es físico o matemático y encontró una grave ambigüedad en el artículo, lo invitamos a leer el siguiente párrafo.Cuando hablamos de «curvatura» nos referimos a la curvatura gaussiana o a la curvatura seccional (que, como usted bien sabrá de sus cursos de geometría riemanniana, coinciden en dimensión dos). No consideramos necesario especificarlo, pues significaría introducir nomenclatura adicional que no aporta nada a la discusión.
Referencias
[1] Killing, W. (1891). «Ueber die Clifford-Klein’schen Raumformen». Mathematische Annalen, Springer Berlin / Heidelberg. Disponible acá.
[2] Hopf, H. (1926). «Zum Clifford-Kleinschen Raumproblem». Mathematische Annalen, Springer Berlin / Heidelberg. Disponible acá.
[3] Gauss, C. F. (1828). «Disquisitiones generales circa superficies curvas». Typis Dieterichianis. Disponible acá.